Objetośc bryły ograniczonej Prestran: Witam, mam do policzenia objętość brył ograniczonej powierzchniami: z= a² − x² y=2x x+y=a z=0 y=0 Użyć muszę całki podwójnej i wzoru na objętość przy jej wykorzystaniu. Nie mogę jednak znaleźć granic całek, a zwłaszcza dla całki od x. Dla y ustaliłem 0 i 2x.

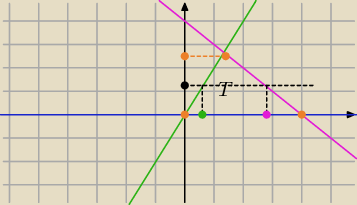
Gray: Zakładam, że a>0, dla a<0 podobnie. Prosta różowa: y=a−x. Prosta zielona: y=2x. Prosta niebieska: y=0.

	a
Całkujesz po trójkącie T. Łatwiej najpierw po y. Zmienna y zmienia się od 0 do		(to
	3

górna pomarańczowa kropka na osi Oy). Dla ustalonego y (czarna kropka), x zmienia się od y/2 (zielona kropka) do a−y (różowa kropka). Mamy więc V=∫∫_T(a²−x²)dxdy = ∫_[0,a/3] ∫_{[y/2, a−y]} (a²−x²)dx dy = ... Dalej Ty.