Moje propozycje zapisu wyrażeń i liczb
Gustlik:
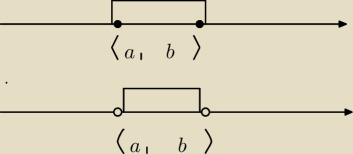
Chciałem przedstawić moje propozycje zmian zapisu niektórych wyrażeń algebraicznych, co
wyeliminowałoby część błędów u uczniów:
1. Sumy algebraiczne powinny być obligatoryjnie zapisywane w nawiasach, z wyjątkiem sytuacji
gdy taka suma jest wynikiem jakiegoś działania. A już nawiasy powinny być OBOWIĄZKOWE, jeżeli
taka suma występuje w ułamkach, wykładnikach potęg i pierwiastkach.
| | x+3 | | (x+3) | | x−2 | |
Np. zamiast pisać |
| powinno się pisać |
| , zamiast |
| powinno się |
| | 2 | | 2 | | x+4 | |
| | (x−2) | |
pisać |
| . To samo z potęgami − zamiast 2x+4 = 2(x+4) i pierwiastkami |
| | (x+4) | |
√x−3=
√(x−3). Dlaczego powinny być takie zmiany? Z prostej przyczyny − taki zapis jest o
wiele bardziej przejrzysty, a zwłaszcza dla uczniów, bo uczeń wtedy widzi "nawias" i wie, że z
takim wyrażeniem musi postępować "jak z nawiasem", czyli jeżeli np. stoi wcześniej minus − to
zmienia on znaki wszystkich składników sumy, jak mnożymy to przez liczbę, to tak jakbyśmy
mnożyli "nawias" przez liczbę, jak mnożymy przez inną sumę (też zapisaną wtedy w nawiasie) to
mnożymy "jak nawias przez nawias". Uczeń wtedy widzi, że te wyrażenia "zachowują się jak
nawiasy", tak je wówczas traktuje i nie robi błędów. Natomiast jak nie ma nawiasu, to uczeń
traktuje te wyrażenia jak wyrażenia bez nawiasu i robi błędy, np. zapomina o zmianie znaków w
calym wyrażeniu "bo nie ma nawiasu", np.
| x+3 | | x+4 | | x+3−x+4 | | 7 | |
| − |
| wielu uczniów zapisuje tak: |
| = |
| i jest już błąd. |
| 2 | | 2 | | 2 | | 2 | |
Albo np. mnoży tylko pierwszy wyraz przez liczbę stojącą przed takim wyrażeniem, np.
| | x+4 | | 3x+4 | | (x+4) | |
3* |
| = |
| , bo "nie ma nawiasu". A gdyby zapisać tak: 3* |
| to wiadomo, że |
| | 4 | | 4 | | 4 | |
| | (3x+12) | |
trzeba mnożyć to "jak nawias przez liczbę", czyli |
| i jest przejrzyściej i nie ma |
| | 4 | |
błędu.
Pisząc te sumy w nawiasie uczeń zrobi prawidłowo:
| (x+3) | | (x+4) | | (x+3)−(x+4) | | (x+3−x−4) | | −1 | | 1 | |
| − |
| = |
| = |
| = |
| =− |
| . |
| 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
Podobnie z potęgowaniem, np. (2
x+3)
x+4 bez nawiasów uczeń zrobi tak:
2
x+3*x+4=2
x+3x+4=2
4x+4 i jest źle, a przejrzyściej wygąda tak:
(2
(x+3))
(x+4)=2
(x+3)*(x+4) i już wiadomo, ze wykładniki mnożymy jak "dwa nawiasy"
czyli każdy z każdym. Podobnie jest z czymś takim:
√√2+3*
√√2+4, uczeń nie wie nieraz
jak to mnozyć. Gdyby był taki zapis:
√(√2+3)*
√(√2+4) to wiadomo, ze wyrażenia pod
pierwiastkami "mnożymy jak dwa nawiasy".
2. Z chwilą pojawienia się liczb ujemnych, a wiec jeszcze w szkole podstawowej należałoby nieco
zmienic kolejność wykonywania działań. Nie nawiasy na pierwszym miejscu, a SPRAWDZANIE ZNAKÓW

!
Czyli kolejność działań powinna być taka:
1. Sprawdzanie znaków  !
! i to powinno być mocno zaakcentowane przez zarówno autorów
podręczników jak i nauczycieli

! Czynność ta ma bezwzględne pierwszeństwo, nawet przed
nawiasami.
2. Nawiasy.
3. Potęgi i pierwiastki.
4. Mnożenie i dzielenie.
5. Dodawanie i odejmowanie.
Taki sposób eliminuje u uczniów błędy znakowe − uczeń ma wpojone, że zanim zacznie cokolwiek
liczyć, to sprawdza znaki liczb czy wyrażeń algebraicznych i w większości wypadków liczy
prawidłowo.
3. Przedziały − jak na rysunku − domknięty to kropki wewnątrz przedziału, bo zawiera końce,
otwarty − kropki na zewnątrz, bo nie zawiera końców. Ja stosuję ten sposób i dzięki temu
wyeliminowałem często popełniane przez uczniów błędy przy działaniach na przedziałach − pisał
o tym kiedyś
Bogdan. Ten szkolny sposób jest z gruntu zły i zmyla uczniów.
18 sty 22:02
Saizou :
a ja się nie zgodzę, bo im mniej znaków tym wzór jest bardziej przejrzysty i czytelny
18 sty 22:05
Draghan:
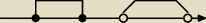
Mnie uczyli, że przy przedziale otwartym są kółeczka niezamalowane i koniecznie kreski pochyłe
do środka przedziału, zaś przy zamkniętym − kółeczka zamalowane i kreski proste, pionowe.

18 sty 22:08
Draghan: A co do nawiasów − ja często przy funkcjach ujmuję argument w nawias − np. nie lubię
"swobodnych iksów" w wyrażeniach z sinusami, logarytmami i innymi. Ale to taka bardziej
naleciałość z programowania.
18 sty 22:10
Gray: Draghan, ja tak w przedszkolu pociąg rysowałem...
18 sty 22:10
Gustlik: Draghan, wiem, znam to ale to też nie jest przejrzyste. Krótko mówiąc − nie sadzi sie
drzew na płocie, bo nie wiadomo czyje to drzewo i awantura między sąsiadami pewna. Jeżeli
drzewo ma być nasze, to musi rosnąć u nas na podwórku, może być przy płocie, ale nie może
wystawać na posesję sąsiada. A jeżeli drzewo ma być sąsiada, to musi rosnąć za naszym płotem,
u sąsiada na podwórku i nie może wchodzić na naszą posesję. I podobnie z końcami przedziałów −
jeżeli końce są "nasze" to muszą być "u nas" − przed płotem, a jak "nie nasze" to u "sąsiadów"
− za płotem. Pogadaj z Bogdanem, on Ci powie coś na ten temat. Ja wyeliminowałem u
uczniów błędy tym sposobem, bo uczeń wtedy widzi, gdzie leżą końce i nie pomyli się.
Co do Saizou − dla mnie i Ciebie ten wzór jest przejrzysty, ale uczniowie nie widząc
"nawiasów" nie wiedzą, że z tymi wyrażeniami trzeba tak samo postępować jak z nawiasami i mylą
się. Dla nich przejrzysty jestzapis w nawiasach, gdy go wprowadziłem, to przestali się mylić
np. w rozwiązywaniu równań z takimi wyrazeniami.
18 sty 22:16
Draghan: Gustlik − skoro taka metoda eliminuje błędy uczniów, to znaczy, że coś w tym jest.

Mi
to dobrze wytłumaczono, poza tym mam dość dobrą wyobraźnię i bardzo rzadko zaznaczałem
cokolwiek na osi.
Na jakim poziomie nauczasz?

18 sty 22:20
Gustlik: Od podstawówki aż po studia, ale głównie licealistów.
18 sty 22:20
Draghan: Może kiedyś skorzystam, jeśli będę miał okazję "nauczać" matematyki.

18 sty 22:29
Dziadek Mróz:
Gustlik, ja tej metody używam od kiedy ją tutaj udostępniłeś, czyli od prawie kilku lat i jest
bardzo popularna wśród moich uczniów z korepetycji.
19 sty 11:12
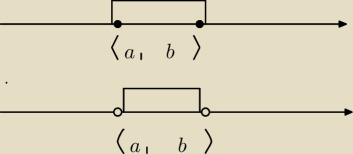 Chciałem przedstawić moje propozycje zmian zapisu niektórych wyrażeń algebraicznych, co
wyeliminowałoby część błędów u uczniów:
1. Sumy algebraiczne powinny być obligatoryjnie zapisywane w nawiasach, z wyjątkiem sytuacji
gdy taka suma jest wynikiem jakiegoś działania. A już nawiasy powinny być OBOWIĄZKOWE, jeżeli
taka suma występuje w ułamkach, wykładnikach potęg i pierwiastkach.
Chciałem przedstawić moje propozycje zmian zapisu niektórych wyrażeń algebraicznych, co
wyeliminowałoby część błędów u uczniów:
1. Sumy algebraiczne powinny być obligatoryjnie zapisywane w nawiasach, z wyjątkiem sytuacji
gdy taka suma jest wynikiem jakiegoś działania. A już nawiasy powinny być OBOWIĄZKOWE, jeżeli
taka suma występuje w ułamkach, wykładnikach potęg i pierwiastkach.
 !
Czyli kolejność działań powinna być taka:
1. Sprawdzanie znaków
!
Czyli kolejność działań powinna być taka:
1. Sprawdzanie znaków  ! i to powinno być mocno zaakcentowane przez zarówno autorów
podręczników jak i nauczycieli
! i to powinno być mocno zaakcentowane przez zarówno autorów
podręczników jak i nauczycieli  ! Czynność ta ma bezwzględne pierwszeństwo, nawet przed
nawiasami.
2. Nawiasy.
3. Potęgi i pierwiastki.
4. Mnożenie i dzielenie.
5. Dodawanie i odejmowanie.
Taki sposób eliminuje u uczniów błędy znakowe − uczeń ma wpojone, że zanim zacznie cokolwiek
liczyć, to sprawdza znaki liczb czy wyrażeń algebraicznych i w większości wypadków liczy
prawidłowo.
3. Przedziały − jak na rysunku − domknięty to kropki wewnątrz przedziału, bo zawiera końce,
otwarty − kropki na zewnątrz, bo nie zawiera końców. Ja stosuję ten sposób i dzięki temu
wyeliminowałem często popełniane przez uczniów błędy przy działaniach na przedziałach − pisał
o tym kiedyś Bogdan. Ten szkolny sposób jest z gruntu zły i zmyla uczniów.
! Czynność ta ma bezwzględne pierwszeństwo, nawet przed
nawiasami.
2. Nawiasy.
3. Potęgi i pierwiastki.
4. Mnożenie i dzielenie.
5. Dodawanie i odejmowanie.
Taki sposób eliminuje u uczniów błędy znakowe − uczeń ma wpojone, że zanim zacznie cokolwiek
liczyć, to sprawdza znaki liczb czy wyrażeń algebraicznych i w większości wypadków liczy
prawidłowo.
3. Przedziały − jak na rysunku − domknięty to kropki wewnątrz przedziału, bo zawiera końce,
otwarty − kropki na zewnątrz, bo nie zawiera końców. Ja stosuję ten sposób i dzięki temu
wyeliminowałem często popełniane przez uczniów błędy przy działaniach na przedziałach − pisał
o tym kiedyś Bogdan. Ten szkolny sposób jest z gruntu zły i zmyla uczniów.
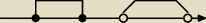 Mnie uczyli, że przy przedziale otwartym są kółeczka niezamalowane i koniecznie kreski pochyłe
do środka przedziału, zaś przy zamkniętym − kółeczka zamalowane i kreski proste, pionowe.
Mnie uczyli, że przy przedziale otwartym są kółeczka niezamalowane i koniecznie kreski pochyłe
do środka przedziału, zaś przy zamkniętym − kółeczka zamalowane i kreski proste, pionowe.

 Mi
to dobrze wytłumaczono, poza tym mam dość dobrą wyobraźnię i bardzo rzadko zaznaczałem
cokolwiek na osi.
Na jakim poziomie nauczasz?
Mi
to dobrze wytłumaczono, poza tym mam dość dobrą wyobraźnię i bardzo rzadko zaznaczałem
cokolwiek na osi.
Na jakim poziomie nauczasz? 
