Zadanie maturalne Dżepetto 18: Wyznacz wszystkie wartości parametru a, dla których równanie ||x−3| −2| = a ma dokładnie trzy pierwiastki. |x−3| −2 = a i |x−3| −2 = −a x−3 = a+2 i x−3 = −a−2 i x−3 = −a+2 i x−3 = a−2 x=a+5 i x=1−a i x=5−a i x=a+1 Ktoś nakieruje jak wyznaczyc tylko 3 parametry a?

Ada: Spójnikiem jest tu lub ! Kiedy np. x₁=x₂ i x₂≠x₃≠x₄

Dżepetto 18: Wybacz, mylę kiedy wstawić lub/i. Odnośnie wskazówki wiem o tym lecz nadal nie mogę wpaść Ps. odpowiedź to a=2

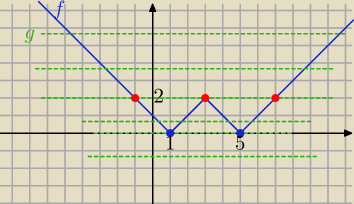
Eta: Graficznie : f(x)= ||x−3|−2| i g(x)= a dla a=2 równanie f(x)= a ma trzy rozwiązania

Dżepetto 18: Dziękuję Eta, wszystko ślicznie narysowane

Eta: ...... tylko odzew z jednodniowym opóźnieniem

PW: No już tak się nie zamartwiaj

Eta: @ Dżepett18 zad / Wyznacz liczbę rozwiązań równania ||x−3|−2|=a w zależności od parametru "a" i narysuj wykres g(a)