relacje ola: W zbierze X wszystkich funkcji określonych na ℛ o wartościach w ℛ niech dana będzie relacja częściowego porządku ≤: ∀f,g∊X : f ≤ g ⇔ ∀x∊ℛ : f(x) ≤ g(x). (a) Czy funkcje x→e^x oraz x→ sin x są porównywalne względem tej relacji? (b) Wskazać na rysunku funkcje, które są większe od x→sinx względem tej relacji? proszę o pomoc, albo chociaż jakieś wskazówki co zrobić

ola: czy chodzi o to, że np. f: x→e^x, a g: x→sinx czyli czy f(x)≤ g(x) czyli czy zbiór wartoście funkcji f jest mniejszy od g(x), a że zbiór wartości g(x): (0, +∞) a f(x) to od <1,−1> tzn. że nie są porównywalne wg tej relacji? proszę o pomoc

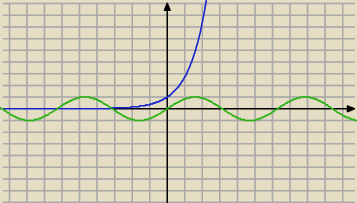
Gray: Nie. Chodzi o to, czy wykres funkcji e^x leży zawsze nad wykresem funkcji sinx (lub się pokrywają). Na rysunku niebieskie to e^x, zielone sin(x). Widać, że dla x≥0 jest OK, dla dla x<0 już nie. Więc te funkcje nie są porównywalne. Porównywalne z funkcją sin będą te funkcje których wykres będzie zawsze nad (lub pod) sinusem; ewentualnie mogą się "momentami" pokrywać.

ola: dzięki

ola: czyli na przykład funkcją porównywalną z funkcją sin może być x→x²+1?

Gray: Tak. Może też być np. x→−x²−1.

ola: jeszcze raz dziękuje