jak to ugryść :D
Krzysiek: W trapezie ABCD o podstawach AC i CD dane sa wierzchołki A(−5,1) B(3,−3) i C(3,1). Przekątna DB
trapezu jest zawarta w prostej 3x+2y=3. Oblicz współrzędne punktu D, sinus BAD oraz promień
okręgu opisanego na trójkącie ABD.
1) nie wiem jak obliczyć ten punkt D

więc zacząłem od narysowania tej prostej 3x+2y=3 w
układzie współrzędnych, teraz tak sobie na to patrze i nie wiem czy dobrze myślę ale według
mnie tutaj są dwie możliwości dla punktu D
I) tworzy się go w taki sposób aby proste AB i BC były równoległe
II) tworzy się go w taki sposób aby proste AB i DC były równoległe
Moje pytanie, mam rację? Jak mogę obliczyć ten punkt D 
18 sty 16:56
Krzysiek:
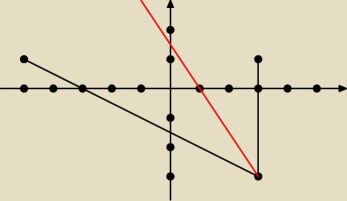
18 sty 17:01
Eta:
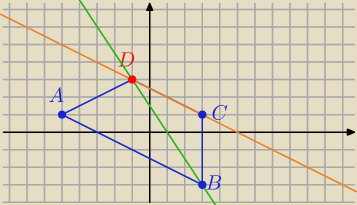
→
AB=[8,−4] prosta AB ⊥ prostej DC i C(3,1)
to DC: 1(x−3)+2(y−1)=0 ⇒ x+2y=5
rozwiąż układ równań
otrzymasz .......
D(−1,3)
18 sty 17:48
Janek191:
Np.
D = ( x; y)
→ →
AB = DC
[ 8 ; − 4 ] = [ 3 − x ; 1 − y ]
8 = 3 − x i − 4 = 1 − y
x = − 5 i y = 5
D = ( − 5; 5)
=========
18 sty 17:50
Janek191:
Wróć − miał być trapez , a nie równoległobok

18 sty 17:51
Krzysiek: tak też mi wychodzi z rysunku ale czy nie może być drugiej sytuacji gdy
AD ⊥ do BC ?
18 sty 17:53
Krzysiek: To wyżej to do
Eta 
18 sty 17:54
Eta:
Wtedy D∉BC
18 sty 17:55
Krzysiek: nie rozumiem

18 sty 17:57
Krzysiek: przecież przedłużając prostą BD (3x+2y=3) na pewno kiedyś napotka ona taki punkt D aby AD było
⊥ do BC

18 sty 17:59
Eta:
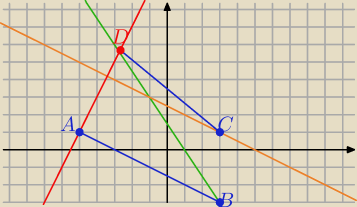
Gdyby tak było to:
Czy wtedy AB∥ DC ?
wniosek ......... ABCD nie jest trapezem !
18 sty 18:10
Krzysiek:
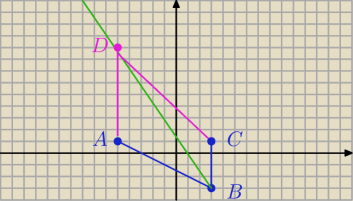
o to mi chodziło (o równoległość AB do DC )czy tak nie może być ?

wtedy D miał by (−5,9)
18 sty 18:27
Eta:
Jasne ,że może

Nie wiedziałam o co pytasz?
18 sty 18:33
Krzysiek: teraz widzę u góry że gdzieś zamiast ∥ dałem ⊥ stąd to nieporozumienie

podsumowując są możliwe dwa rozwiązania, więc w dalszej części muszę je uwzględniać
18 sty 18:43
 więc zacząłem od narysowania tej prostej 3x+2y=3 w
układzie współrzędnych, teraz tak sobie na to patrze i nie wiem czy dobrze myślę ale według
mnie tutaj są dwie możliwości dla punktu D
I) tworzy się go w taki sposób aby proste AB i BC były równoległe
II) tworzy się go w taki sposób aby proste AB i DC były równoległe
Moje pytanie, mam rację? Jak mogę obliczyć ten punkt D
więc zacząłem od narysowania tej prostej 3x+2y=3 w
układzie współrzędnych, teraz tak sobie na to patrze i nie wiem czy dobrze myślę ale według
mnie tutaj są dwie możliwości dla punktu D
I) tworzy się go w taki sposób aby proste AB i BC były równoległe
II) tworzy się go w taki sposób aby proste AB i DC były równoległe
Moje pytanie, mam rację? Jak mogę obliczyć ten punkt D 

 →
AB=[8,−4] prosta AB ⊥ prostej DC i C(3,1)
to DC: 1(x−3)+2(y−1)=0 ⇒ x+2y=5
rozwiąż układ równań
→
AB=[8,−4] prosta AB ⊥ prostej DC i C(3,1)
to DC: 1(x−3)+2(y−1)=0 ⇒ x+2y=5
rozwiąż układ równań




 Gdyby tak było to:
Czy wtedy AB∥ DC ?
wniosek ......... ABCD nie jest trapezem !
Gdyby tak było to:
Czy wtedy AB∥ DC ?
wniosek ......... ABCD nie jest trapezem !
 o to mi chodziło (o równoległość AB do DC )czy tak nie może być ?
o to mi chodziło (o równoległość AB do DC )czy tak nie może być ?  wtedy D miał by (−5,9)
wtedy D miał by (−5,9)
 Nie wiedziałam o co pytasz?
Nie wiedziałam o co pytasz?
 podsumowując są możliwe dwa rozwiązania, więc w dalszej części muszę je uwzględniać
podsumowując są możliwe dwa rozwiązania, więc w dalszej części muszę je uwzględniać