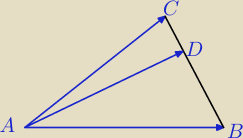
 Na boku BC trójkąta ABC obrano punkt D, taki że |BD| do |DC| = a do b (BD i DC to wektory),
gdzie a i b ∊ R+ . Wykaż, że wektor AD= 1a+b(a*AC+b*AB) −AC i AB to też wektory.
Nie mam zielonego pojęcia jak się za to zabrać. Proszę o jakąś wskazówkę..
Na boku BC trójkąta ABC obrano punkt D, taki że |BD| do |DC| = a do b (BD i DC to wektory),
gdzie a i b ∊ R+ . Wykaż, że wektor AD= 1a+b(a*AC+b*AB) −AC i AB to też wektory.
Nie mam zielonego pojęcia jak się za to zabrać. Proszę o jakąś wskazówkę..
| BD | a | ||
= | ? | ||
| DC | b |
 nie wiedziałam jak to tutaj zapisać.
nie wiedziałam jak to tutaj zapisać.

| a | b | |||
z warunków zadania BD→= | BC→ i DC→= | BC→ | ||
| a+b | a+b |
| a | b | |||
⇒ AD→= AB→+ | BC→ /* b i AD→= AC→ − | BC→ /* a ⇔ | ||
| a+b | a+b |
| ab | ab | |||
⇔ bAD→=bAB→+ | BC→ i aAD→=aAC→ − | BC→ /+stronami ⇒ | ||
| a+b | a+b |
