Zadanie nr 4-funkcje 5-latek: Niech f(x)=[|x|] i g(x)=|[x]| ,sprawdz ze dla x∊<0,∞) zachodzi rownosc f(x)=g(x) . czy funkcje fi g sa rowne na calej prostej?

5-latek: Na tym przedziale |x|=x dla x≥0 wiec [|x|]=[x} i |[x]|= [x] Nie rozuniem tego czy one sa rowne na calej prostej .

Eve: cos mnie zamroczyło, co to f(x)=[IxI]?

5-latek: Pewnie Eve czesc calkowita liczby z jej wartosci bezwzglednej

5-latek: |[x]| ja to odczytuje jak wartosc bewzgledna z czesci calkowitej liczby

Eve: no tak

Eve:

	l
f(x)=[In+		I]=[InI]=n v 0
	m

	l
g(x)=I[n+		]I=InI=n v 0
	m

czyli?

5-latek: Sa one rowne na tym przedziale . Chodzi mi bardziej o to czy one sa rowne na calej prostej (tego nie rozumiem ) Dlaczego ? dlatego ze wykresem czesci liczby calkowitej sa odcinki a nie prosta

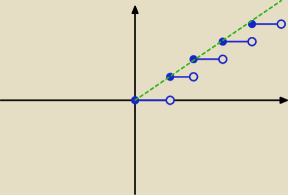
Eve: może chodzi o tę prostą? ale nie jestem pewna

5-latek: Eve Tez myslalem o tej . Moze zapytam Graya jak sie pojawi na forum .

Eve: bo wtedy oznaczałoby, że są równe, próbuje znaleźć kontprzykład, ale całości liczb bez względu na część ułamkową sa równe

Gray: Jest OK, tj. dla x≥0 macie f(x)=g(x) − to pokazaliście. Pytanie "czy funkcje f i g sa rowne na całej prostej?" należy rozumieć tak: czy funkcje f i g są równe dla wszystkich x∊R (autorowi zadania chodzi tu na pewno o prostą rzeczywistą tj. oś Ox − tak się ją czasami nazywa).