Standaryzacja CKE
Krzysiek: Standaryzacja CKE
Witam, ostatnio brałem udział w standaryzacji CKE − chyba tak to się nazywa i natrafiłem na
nietypowe dla mnie zadanie. Nie jestem pewny czy dobrze zapamiętałem ale :
W ostrosłupie prawidłowym ABCDS w którym w podstawie jest kwadrat, na boku |CS| umieszczono
| | 1 | |
punkt P dzielący ten bok na dwie równe połowy. Wiedząc że tangens α kąta ∠CAP wynosi |
| , |
| | 3 | |
oblicz sinus (bądź dokładniej miarę kąta sinus nie jestem pewien) kąta nachylenia krawędzi
bocznej do płaszczyzny podstawy.
Mniej więcej tak to wyglądało, możliwe że gdzieś źle zapamiętałem, więc fajnie by też było
gdyby osoby biorące udział w tej standaryzacji dopomogły z treścią. Według mnie jest ona na
99% prawdziwa.

16 sty 17:00
Krzysiek:
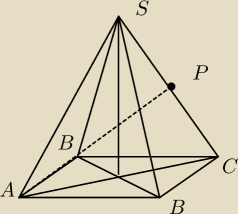
rysunek dałem taki i dalej nie wiem co

nie umiem zaznaczać tutaj kątów to nie zaznaczę

16 sty 17:06
Krzysiek: Ktoś coś

17 sty 10:48
Janek191:
Na krawędzi CS wybrano punkt P dzielący odcinek CS na połowy.
Połowy są zawsze równe !

Boki występują w wielokątach

18 sty 08:48
daras: kiedyś słyszałem od matematyka o większej połowie

musi więc by i mniejsza
18 sty 09:27
Krzysiek: @Janek191
Wiem, że połowy są równe zaznaczyłem to w treści zadania żeby nie było jasne
18 sty 11:36
Krzysiek:
19 sty 18:39
Krzysiek:
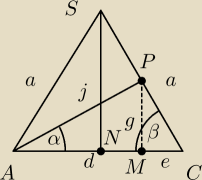
Δ NCS ∼ Δ MCP
| | 1 | |
skoro CP to |
| a więc CS to a |
| | 2 | |
| | 1 | |
co więcej NM |
| e a to NC = e |
| | 2 | |
e=d
chyba tutaj wypadało by uruchomić tw. Pitagorasa

AC = 2e
i tutaj już mam gdzieś stop nie wiem co by tu dalej bo jakieś głupoty wychodzą mi

20 sty 17:25
Krzysiek:
25 sty 18:19

 rysunek dałem taki i dalej nie wiem co
rysunek dałem taki i dalej nie wiem co  nie umiem zaznaczać tutaj kątów to nie zaznaczę
nie umiem zaznaczać tutaj kątów to nie zaznaczę 

 Boki występują w wielokątach
Boki występują w wielokątach 
 musi więc by i mniejsza
musi więc by i mniejsza
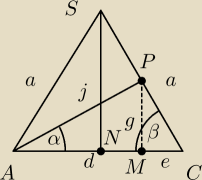
 AC = 2e
AC = 2e
