Nierówności, funkcja kwadratowa i równanie kwadratowe Mr0w4: https://fbcdn-sphotos-h-a.akamaihd.net/hphotos-ak-xpa1/v/t34.0-12/10937425_915671385132593_2037918853_n.jpg?oh=5cbf31d4dd2620b09cb0ed1fc052c009&oe=54BA7C06&__gda__=1421568806_5668af3cb359afedb02d0e260406f74d https://fbcdn-sphotos-h-a.akamaihd.net/hphotos-ak-xpa1/v/t34.0-12/967957_915671401799258_2116530301_n.jpg?oh=ed4b2ec08b4f920edac009c2b10c4e40&oe=54BA7BFF&__gda__=1421507172_a152059e7a08a6538e63ce0ca2003e18 Byłby ktoś w stanie mi to rozwiązać? To nie jest trudne ale chciałbym mieć 100% pewności że dobrze sam to rozwiązałem.

Janek191: z.1 x² − 3 x + 2 = 0 ( x − 1)*( x − 2) = 0 x = 1 lub x = 2 ============ ( x + 8)*( x − 4) = 0 x + 8 = 0 lub x − 4 = 0 x = − 8 lub x = 4 ================= x³ − 5 x² + 6 = 0 x = − 1 jest jednym z rozwiązań tego równania, bo ( − 1)³ − 5*( −1)² + 6 = − 1 − 5 + 6 = 0 zatem x³ − 5 x² + 6 dzieli się przez ( x + 1) Wykonujemy to dzielenie: ( x³ − 5 x² + 6) : ( x + 1) = x² − 6 x + 6 − x³ − x² −−−−−−−− − 6 x² + 6 6 x² + 6 x −−−−−−−−−− 6 x + 6 − 6 x − 6 −−−−−−−−− 0 oraz x² − 6 x + 6 = 0 Δ = 36 − 4*1*6 = 36 − 24 = 12 = 4*3 √Δ = 2√3

	6 − 2√3
x =		= 3 − √3 lub x = 3 + √3
	2

Odp. x = − 1 lub x = 3 − √3 lub x = 3 + √3 ========================================

3 x − 1
	= 4 x / * 2
2

3 x − 1 = 8 x − 1 = 5 x x = − 0,2 ======= x³ − 3 x² + 4 x −12 = 0 x²*( x − 3) + 4*( x − 3) = 0 ( x − 3)*( x² + 4) = 0 x − 3 = 0 x² + 4 > 0 dla x ∊ ℛ x = 3 ===== Czy to jest sprawdzian ?

Janek191: Wstaw swoje rozwiązania, to sprawdzimy ich poprawność

Mr0w4: Egzamin semestralny w II LO dla dorosłych 1 zadanie mam tak samo. Chcę sobie zrobić w razie w. gotowe do przepisania rozwiązania, siedzę i rozwiązuję. 3 x − 1 = 4 x / * 2 2 3 x − 1 = 8 x − 1 = 5 x x = − 0,2 ======= x3 − 3 x2 + 4 x −12 = 0 x2*( x − 3) + 4*( x − 3) = 0 ( x − 3)*( x2 + 4) = 0 x − 3 = 0 x2 + 4 > 0 dla x ∊ ℛ x = 3 ======= To mam źle rozwiązałem, ale dziękuję. Z tej 2 kartki zalezy mi na 4,5,6 i 8 zadaniu bo logarytmy mam na świeżo.

Mr0w4: Chcę tylko skończyć tą szkołe i mieć średnie, ponieważ w pracy wymagają tego odemnie. :v tak to w życiu bym nie wrócił już do szkoły

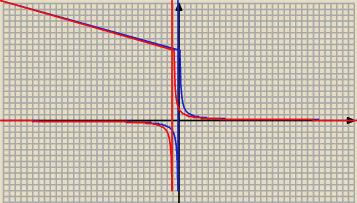
Janek191: z.2

	2
y =		; x ≠ − 1
	x + 1

Wykresem jest hiperbola − kolor czerwony

	2
Otrzymujemy ją z wykresu funkcji y =		po przesunięciu o wektor
	x

→ w = [ − 1; 0 ] Na wykresie nie powinno być tej skośnej półprostej .

Janek191: z.3 a)

3 x − 2		x
	<		/ * 6
2		3

3*( 3 x − 2) < 2 x 9 x − 6 < 2 x 9 x − 2 x < 6 7 x < 6 / : 7

	6
x <
	7

========= b)

4
	> 5 ; x ≠ 0
x

4
	− 5 > 0
x

4		5 x
	−		> 0
x		x

4 − 5 x
	> 0
x

x*( 4 − 5 x) > 0

	4
x1 = 0 x2 =
	5

Z wykresu funkcji y = x*( 4 − 5x) = − 5 x² + 4 x ; a = − 5 < 0 odczytujemy rozwiązania nierówności:

	4
x ∊ ( 0 ;		)
	5

===============

Mr0w4: Wielkie dzięki