Liczby zespolone
majkel: Sprawdź, czy liczba z=(3−i)/(1−
√3)
5
należy do zbioru |2+i−z|>=|z−1|
Odpowiedź uzasadnij.
Proszę o pomoc, brakuje mi pomysłów

15 sty 23:55
Draghan: A jak podstawisz
z do nierówności...?

15 sty 23:56
majkel: Tzn.? Ten pierwiastek 5 stopnia mnie trochę demotywuje. Ciężko idą mi te zespolone, oj
ciężko...
15 sty 23:58
Draghan: Hmm... Ja bym się tam nie przejmował tym ułamkiem. Rozszerzyłbym wszystkie liczby z nierówności
do ułamka o mianowniku (1−
√3)
5.

Chyba że tak nie można.

Ale przynajmniej spróbuj.

Zespolone nie są trudne.

Najwięcej problemów z wyznaczaniem kąta, na resztę są wzory.

16 sty 00:07
majkel: no własnie przeszkadza mi ten pierwiastek przy liczeniu modułu
16 sty 00:14
Draghan: To rozpisz z dwumianu Newtona.

16 sty 00:22
Draghan: Ale jak patrzę na polecenie, to wydaje mi się, że można jakoś prościej... Tylko trzeba na to
wpaść.

Ktoś inny ma jakiś pomysł?

16 sty 00:28
majkel: o matko, z dwumianem to chyba jeszcze większa komplikacja... kurcze, głupi jestem, naprawdę
16 sty 00:30
Draghan: Komplikacja, komplikacją − ale rozwiązanie będziesz miał.

A może wystarczy oszacować?

16 sty 00:31
majkel: Hmmm z szacowaniem raczej ciężko. Po prostu jest coś, czego nie potrafię dostrzec

16 sty 00:39
Draghan: Poczekaj, może nie trzeba liczyć tego pierwiastka. Daj mi chwilę, rozpiszę sobie tę nierówność.

16 sty 00:45
majkel: OK, rano spojrzę jaki efekt. Dziękuje bardzo
16 sty 00:48
Draghan: | | 3−i | | 3 | | −1 | |
z = |
| = a + bi, gdzie a = |
| , b = |
| |
| | (1−√3)5 | | (1−√3)5 | | (1−√3)5 | |
Może dla ułatwienia, oznaczmy (1−
√3)
5 jako stałą x (x < 0).
Teraz rozpiszę dwa moduły z nierówności, a wnioski spróbuj wyciągnąć samodzielnie.

|2 + i − z| = |2 + i − (a + bi)| = |2 − a + i − bi| =
√ (2 − a)2 + (1 − b)2 = (...)
| | 10 | | 10 | |
(...) = (5 − |
| + |
| )12 //zmieniłem pierwiastek na potęgę, bo w zapisie |
| | x | | x2 | |
na stronce coś nie działało...
| | 7 | | 9 | |
|z − 1| = |a − 1 + bi| = (...) = (1 − |
| + |
| )12 |
| | x | | x2 | |
Teraz można jako−tako oszacować, pamiętając że x < 0 (ważne przy x
2 
).
16 sty 01:11
Gray: | | 3−i | |
Na 99,(9)% w mianowniku kolego zapomniał i, tzn. powinno być |
| , lub coś |
| | (1−i√3)5 | |
podobnego (może (i−
√3)
5). Wtedy do prawej strony należałoby wypalić z armaty de Moivre'a.
Zadanie w takiej postaci jak jest (tj. bez i) nie ma "tego czegoś", co powinno być w każdym
szanującym się zadaniu.
16 sty 10:09
majkel: Nie ma i w mianowniku.
16 sty 15:49
majkel: Na pewno nie popełniłem tutaj błędu, przepisałem przykład dobrze.
16 sty 15:50
MQ:
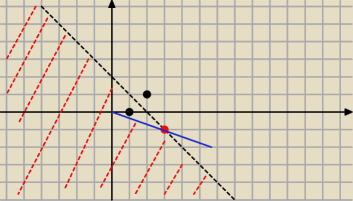
Nierówność
|2+i−z|>=|z−1|
oznacza półpłaszczyznę rozdzieloną symetralną odcinka między punktami z
1=2+i oraz z
2=1, w
której leży punkt z
2.
Trzeba tylko sprawdzić,czy w tej półpłaszczyźnie leży rzeczona liczba.
3−i, jak widać (czerwony punkt), leży na tej symetralnej, ale mamy jeszcze dzielenie przez
(1−
√3)
5.
| | 1 | |
Ponieważ 1−√3<1, więc (1−√3)5<1, czyli |
| >1, a zatem odległość badanej |
| | (1−√3)5 | |
liczby od środka płaszczyzny zespolonej (p. 0) jest większa niż liczby 3−i.
Stąd wniosek (patrząc na rysunek i niebieską linię), że badana liczba leży poza obszarem
czerwonym, więc nie spełnia nierówności.
16 sty 16:17


 Chyba że tak nie można.
Chyba że tak nie można.  Ale przynajmniej spróbuj.
Ale przynajmniej spróbuj.  Zespolone nie są trudne.
Zespolone nie są trudne.  Najwięcej problemów z wyznaczaniem kąta, na resztę są wzory.
Najwięcej problemów z wyznaczaniem kąta, na resztę są wzory. 

 Ktoś inny ma jakiś pomysł?
Ktoś inny ma jakiś pomysł? 
 A może wystarczy oszacować?
A może wystarczy oszacować? 


 |2 + i − z| = |2 + i − (a + bi)| = |2 − a + i − bi| = √ (2 − a)2 + (1 − b)2 = (...)
|2 + i − z| = |2 + i − (a + bi)| = |2 − a + i − bi| = √ (2 − a)2 + (1 − b)2 = (...)
 ).
).
 Nierówność
|2+i−z|>=|z−1|
oznacza półpłaszczyznę rozdzieloną symetralną odcinka między punktami z1=2+i oraz z2=1, w
której leży punkt z2.
Trzeba tylko sprawdzić,czy w tej półpłaszczyźnie leży rzeczona liczba.
3−i, jak widać (czerwony punkt), leży na tej symetralnej, ale mamy jeszcze dzielenie przez
(1−√3)5.
Nierówność
|2+i−z|>=|z−1|
oznacza półpłaszczyznę rozdzieloną symetralną odcinka między punktami z1=2+i oraz z2=1, w
której leży punkt z2.
Trzeba tylko sprawdzić,czy w tej półpłaszczyźnie leży rzeczona liczba.
3−i, jak widać (czerwony punkt), leży na tej symetralnej, ale mamy jeszcze dzielenie przez
(1−√3)5.