aa
Hugo: Hugo z Przebiegiem: Legenda Prawdziwa.
Dokonaj przebiegu funkcji dla:
1. y= x −ln(x+1)
5. y = e
1/x − x
6. y = x
2 −4|x|+3
8. y = x−2arctgx
9. y=ln(sinx) // zakladam ze tu jest () a nie modulo : > bo mam troszcze nieczytelnie
10. y=x
2 * e
−x^^
2 /e do potęgi −x
2
1 Dziedzinę.
2 Miejsca zerowe.
3 Punkt przecięcia z osią Oy.
4 Granice na krańcach dziedziny. //** to tez? w etrapezie takiego czegos nie ma
5 Asymptoty.
6 Przedziały monotoniczności.
7 Ekstrema.
8 Przedziały wklęsłości i wypukłości.
9 Punkty przegięcia.
tabelka
15 sty 14:50
15 sty 14:59
Hugo: zatem
1. Dziedzina
2. Asymptoty
3. Ekstrema
4. Wklęsłość
5. Tabelka
15 sty 15:02
5-latek: Ale Hugo to raczej tak:Zbadaj przebieg zmiennosci funkcji
a nie dokonaj .......
15 sty 15:02
5-latek: Jeszcze parzystosc i nieparzystosc funkcji
15 sty 15:03
Hugo:

y = y= x −ln(x+1)
D: x> −1
lim x−> −1
+ x −ln(x+1) = oo
[−1 − log(−oo) = oo

]
zatem istnieje asymptota pionowa prawostronna dla x = −1
| | −ln(x+1) | |
a = lim x−>+− oo f(x) /x = lim x−>+−oo 1 − |
| |
| | x | |
= lim... 0 + 1 = 1 = a
b = limx−>+−oo f(x) − ax =lim... −ln(x+1) = −oo I co teraz

? b jest nie określone
Dziedzina nam wyklucza −oo
[−(ln(oo) ) = − oo]
15 sty 15:16
Hugo: 5−latek : U nas nie wymaga, wiem ze tak jest ale nie wymaga

15 sty 15:17
15 sty 15:19
Hugo:
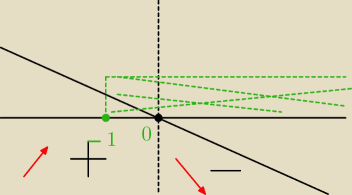
ekstrema:
| | 1 | |
y' = (x −ln(x+1) ) ' = 1 − |
| * 1 |
| | x+1 | |
Df' : x=/= −1 //wiec dalej tak samo

y' = 0
x+1 = 1
x = 0
f(x) rosnąca dla x e (−1 ; 0)
f(x) malejąca dla x e ( 0 ; oo)
ekstrema osiąga maximum w pkt ( 0, 0 )
f(0) = 0
15 sty 15:25
15 sty 15:26
john2: Jeśli chodzi o ukośne, nie ma sensu chyba liczyć przy x −> − ∞, bo nie ma ln(−∞)
b wychodzi ∞ więc nie ma ukośnych
15 sty 15:28
john2: tzn b wychodzi −∞
15 sty 15:28
john2: Na odwrót monotoniczność, minimum w 0
15 sty 15:33
Hugo: źle policzylem

john2
'a' źle mam chyba
| | ln(x+1) | |
lim x−> +−oo x/x − |
| |
| | x | |
| | ln(x+1) | |
lim .. 1 − |
| [oo/oo] |
| | x | |
zatem jedynka znika czy jak

?
15 sty 15:45
Hugo: co na odwrot?!
15 sty 15:45
john2: | | x − ln(x+1) | |
limx−>PLUS∞ |
| = |
| | x | |
| | ln(x+1) | |
= limx−>PLUS∞ [ 1 − |
| ] = ... |
| | x | |
| | ln(x+1) | |
... = limx−>PLUS∞ [ 1 − |
| ] = [1−0] |
| | x | |
15 sty 15:50
Hugo: jedynka znika i a = 0 ? : >
15 sty 15:53
Hugo: czyli dobrze mowilem a = 1
czyli nie istnieje asymptota ukośna

15 sty 15:54
john2: pierwsza pochodna
| | 1 | | x+1 | | 1 | | x | |
y = 1 − |
| = |
| − |
| = |
| |
| | x+1 | | x+1 | | x+1 | | x+1 | |
Badam znak pochodnej
x(x+1) > 0
x ∊ (−
∞, −1)∪(0,+
∞)
uwzględniając dziedzinę
x ∊(0,+
∞)
tam funkcja rośnie
x(x+1) < 0
x∊(−1,0)
tam maleje
15 sty 15:54
john2: Asymptota ukośne wyjdzie jeśli a i b są liczbami (jednocześnie), b nie jest liczbą
15 sty 15:55
Hugo:

1 = 0
brak rozwiązań

15 sty 16:00
john2: tak
15 sty 16:01
Hugo: Cos sie znowu dowiedzialem : ))
a to kolejne :c? tak dziwnie ze same sprzecznosci
15 sty 16:02
Hugo: ok

15 sty 16:02
Hugo: co do tabelki to prosze o pomoc
15 sty 16:02
15 sty 16:11
john2: w ostatnim wierszu sobie rysuj te strzałki tak, jak w tym pdfie
15 sty 16:11
Hugo:
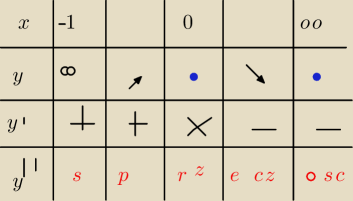
Dziedzina to x e (−1 ; oo) zatem
−1
0 (z liczenia asymptot jako rozwiaanie)
oo
?
15 sty 16:12
Hugo: skoro w y'' wyszla nam sprzecznosc to czemu wszędzie dodattnie


15 sty 16:13
john2: y'' ma znak dodatni, bo
| 1 | |
| jest zawsze dodatnie |
| (x+1)2 | |
15 sty 16:14
Hugo:
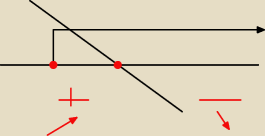
2. czemu masz na odwrót strzałki? funkcja y' przy iksie ma znak minus zatem rysujemy od dolu
zatem musi byc po mojemu?
15 sty 16:17
Hugo: ok

zaskoczyles mnie znowu # y''
ale ta pochodnna y'?
y= x −ln(x+1)
znak jest minus przez iksem a narysowales jak by byl dodatni

15 sty 16:18
john2: zobacz post z 15:54 jeszcze raz
15 sty 16:20
Hugo: Wybacz nie zauważyłem twojego posta − racja wgl przecież nie można przemnażać przez 'x' ,
nalezy wspólny ułamek
15 sty 16:27
Hugo: czyli tam bedzie ekstrema minimum w pkt (0,0)

15 sty 16:30
john2: tak
15 sty 16:51
Hugo: 2)
D xe (0; oo)
asymptoty
| | ln0 | |
lim x−>0− I TU DZIWNE  wychodzi |
| ... czyli −oo/0− czyli oo? |
| | 0− | |
15 sty 16:57
Hugo: i to samo dla 0+ ... −oo
15 sty 16:57
john2: x−>0− nie ma sensu
x−>0+
więc
−∞/0+ = −∞
15 sty 17:00
Hugo: as ukośna
lim x−> +− oo lnx/x / x [−oo/oo] Hospital
w zasadzie ino +oo bo dziedzina
[1/oo] = 0
b = limx−>oo f(x) − ax = lim... lnx/x [−oo/oo]
Hospital
rownanie y = 0x + 0 jest asymptotą ukośną równania (poziomą)
15 sty 17:02
Hugo: Dlaczego nie ma sensu


czyli to mam napisac? że tylko prawostronnie domknięta?
15 sty 17:03
john2: b = ∞
15 sty 17:06
john2: Badamy granice na krańcach dziedziny. Dziedzin to (0, ∞).
Krańcem dziedziny jest zero tylko od prawej strony.
15 sty 17:07
Hugo: racja dziedzina ...
15 sty 17:25
Hugo: teraz pochodne,,, ekstremy
15 sty 17:27
15 sty 17:28
Hugo:
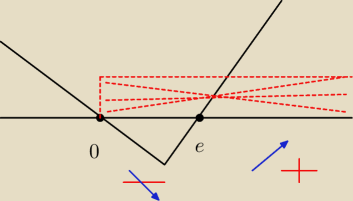
x = 0 v lnx = 0
x = 0 v x = e
f(x) maleje xe (0; e)
f(x) rośnie xe( e; oo)
extremum minimalne dla x = e w punktcie (e, e
− )
15 sty 17:31
john2: źle pochodna
15 sty 17:32
15 sty 17:38
john2: | | lnx | | | | 1 − lnx | |
(x + |
| )' = 1 − |
| = 1 − |
| |
| | x | | x2 | | x2 | |
15 sty 17:40
Hugo:
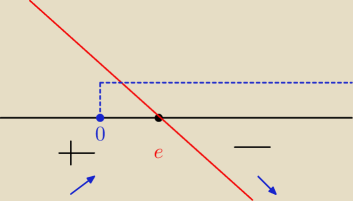
lnx = 1
x = e
przed przekształceniem mamy znak minus przed lnx wiec:
15 sty 17:40
john2: zamiast − jest + po jedynce
15 sty 17:40
Hugo: −,− racja czemu ja nie myśle
x
2 = 1 − lnx
ale co teraz?
15 sty 17:41
john2: | | 1 − lnx | | x2 + 1 − lnx | |
y' = 1 + |
| = |
| |
| | x2 | | x2 | |
15 sty 17:42
Hugo: jezeli zmiana znaków o ile dobrze rozumiem to
−x2 = 1 −lnx
15 sty 17:42
Hugo: ach : )
to od nowa !
przyrównujemy do zera
15 sty 17:42
john2: pochodna chyba jest zawsze dodatnia
15 sty 17:42
Hugo: wymnażamy przez x
2 i zostaje nam
x
2 +1 − lnx = 0
ale co teraz

mamy loga
15 sty 17:43
Hugo: czyli to tak zostawiamy?
15 sty 17:43
john2: funkcja jest rosnąca w całej dziedzinie, brak ekstremów
15 sty 17:45
Hugo:
| | | | 1−lnx | |
y' = 1 + |
| = 1 + |
| |
| | x2 | | x2 | |
15 sty 17:49
Hugo: ok

rosnąca
co do y'' mam nadzieje ze dobrze policzylem
0 = −x + 2x * lnx
15 sty 17:50
Hugo: spekulowałbym że
0 = x( −1 + 2lnx)
x = 0 v 2lnx = 1
x= 0 v lnx = 1/2
x = 0 v x = √e
15 sty 17:51
Hugo:
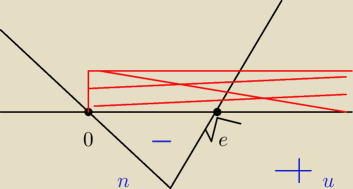
15 sty 17:52
15 sty 17:53
15 sty 17:54
Hugo: f(x) u xe (
√e ; oo)
f(x) n xe (0;
√e)
pkt przegięcia (
√e ,
15 sty 17:56
john2:
−3x + 2xlnx = 0
−x( 3 − 2lnx )= 0
x = 0 lub 3 − 2lnx = 0
−2lnx = − 3
lnx = lne
3/2
x = e
3/2
15 sty 17:59
john2: i badaj znak wyrażenia −3x + 2xlnx
od niego zależy znak drugiej pochodnej
15 sty 18:00
Hugo: jeszcze raz od nowa starannie
| | | | 1 − lnx | |
y' = 1 + |
| = 1 + |
| |
| | x2 | | x2 | |
| | (1 − lnx)' * x2 − 2x* (1 − lnx) | |
y'' = 0 + |
| |
| | x4 | |
15 sty 18:04
Hugo: tzn jak badać?
15 sty 18:05
Hugo:
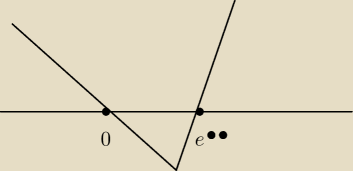
jak dla mnie 2xlog bedzie większy od −3x przez co znak przy jest wazny
15 sty 18:07
Hugo: dobrze

?
15 sty 18:07
john2: dla jakich x
−3x + 2xlnx > 0
i dla jakich x
−3x + 2xlnx < 0
15 sty 18:07
Hugo: a mozna rozwiązywac to graficznie? wole takie ;x
15 sty 18:09
Hugo: tez masz fajne nie trzeba na znak patrzec
15 sty 18:09
john2: −3x + 2xlnx > 0
−x(3 − 2lnx) > 0 / : x, x > 0 znamy znak x
−(3 − 2lnx) > 0 /: (−1)
3 − 2lnx < 0
etc
15 sty 18:09
Hugo: podtrzymuje moje:
f(x) u dla x e (e
3/2 ; oo)
f(x) n dla x e ( 0; e
3/2)
pkt przegięcia dla x = e
3/2
| | lne3/2 | |
f(e3/2) = ee3/2 + |
| |
| | e3/2 | |
15 sty 18:12
Hugo: czyli mam dobrze

?
15 sty 18:12
Hugo: | | 1,5 | |
e3/2 + |
| tak mozna zostawić? //pkt przegięcia |
| | e3/2 | |
15 sty 18:13
john2: ok
przybliżenie kalkulatorem
15 sty 18:14
Hugo: mozna przyblizac? na studiach za to karali
15 sty 18:17
john2: gdzieś na brudno tylko, żebyś mógł ten punkt zaznaczyć na wykresie
15 sty 18:19
Hugo: tabelka:
x // 0 // // e
3/2 // // oo
y'' // x // − // + // + // +
y' // x // + // + // + // + //zawsze dodatnia

!
y // −oo // ↗n // p.przeg(...) // ↗ u // 0
15 sty 18:27
Hugo: dobrze

2/10 zadan

15 sty 18:27
john2: y'' ma wartość zero dla e3/2
15 sty 18:29
john2: i nie wiem co to za 0 na samym koncu tabeli
15 sty 18:30
Hugo: emmm no wiem a co bys tam dal :x? w sumie zasugerowalem sie asymptotą
15 sty 18:32
Hugo: dla lim x−> oo ... tam bylo zero
15 sty 18:33
john2: nic nie pisz tam w wierszu y, jesli nie mamy asymptot poziomych
15 sty 18:36
john2: ale b wyszło nieskończoność, więc odpada
15 sty 18:37
john2: będę za godzinę, rób następne, sprawdzę
15 sty 18:38
Hugo: WIELKIE DZIĘKI TB ! ! !
15 sty 18:44
Hugo: /////////////////////////////////////////////////////// trzecie
Df: xe R/{−2, 2}
lim x−> −2
− = −oo
lim x−> −2
+ = oo
lim x−> 2
− = oo
lim x−> 2
+ = −oo
mamy as pionowe
15 sty 18:57
Hugo: | | x2 | |
lim x−> +−oo f(x) / x = lim... |
| |
| | 4x−x3 | |
lim x−> +−oo f(x) − ax = −1
y = −1 as pozioma
15 sty 19:02
Hugo:
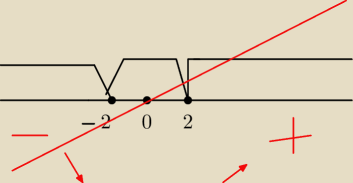
0 = 8x
x = 0

!
f(x) rosnie xe (0;2 ) U (2; oo)
f(x) maleje xe (−oo; −2) U (−2

o)
ekstrema minimalna w pkt (0,0)
15 sty 19:09
john2: wygląda ok
15 sty 19:32
john2: Napisz, jak dokładnie wygląda wzór funkcji numer 4
15 sty 19:33
Hugo: ale jeszcze 3:
druga pochodna jest kopnięta

15 sty 19:35
john2: napisz mi 4, bo chcę już je zacząć robić
15 sty 19:38
Hugo:
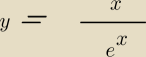
: )))
15 sty 19:39
Hugo:
| | 8(4−x2)2 −8x*2(4−x2) * (−2x) | |
y'' = |
| |
| | (4−x2)2 | |
| | 8(4−x2)[ 4−x2 −(2(−2x)] | |
y'' = |
| |
| | (4−x2)2 | |
| | 8(−x2 + 4x + 4)(4−x2) | |
y'' = |
| |
| | (4−x2)2 | |
15 sty 19:46
Hugo:
| | 8(4−x2)2 −8x*2(4−x2) * (−2x) | |
y'' = |
| |
| | (4−x2)2 | |
| | 8(4−x2)[ 4−x2 −(2x(−2x)] | |
y'' = |
| // iksa zjaslem  |
| | (4−x2)2 | |
| | 8(−x2 + 4 + 4x2)(4−x2) | |
y'' = |
| |
| | (4−x2)2 | |
| | 8( + 4 + 3x2)(4−x2) | |
y'' = |
| |
| | (4−x2)2 | |
15 sty 19:50
Hugo: 3x
2 = −4 SPRZECZNOŚĆ

15 sty 19:50
john2: ok
15 sty 19:51
Hugo:
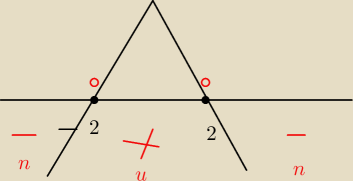
x przy najwyższej ujemny
15 sty 19:51
Hugo: brak wklęsłości/wypuklości bo dziedzina
15 sty 19:56
Hugo: tabelka

!
15 sty 19:57
Hugo:
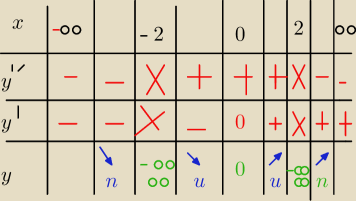
nie wiem co dac dla y

mam wrazene ze tam źle
15 sty 20:09
john2: chyba ok,
w wierszu y pod −∞ i ∞ piszesz rownanie asymptoty ukosnej
napisz tam jeszcze MIN, gdzie f osiaga minimum
15 sty 20:12
Hugo: aaa

15 sty 20:24
Hugo: w pkt zero ma minimum prawda?
15 sty 20:26
Hugo: Mogę spytac jak zadanie 4? : )
15 sty 20:27
john2: tak
15 sty 20:27
Hugo: 5 zadanie mam rozpisane , kyrt... mówił ze by na 6 zobaczył, a końcówkę może coś wyrzebram od
znajomych z klasy
teraz 4

!
oczywiście ślepe przepisywanie jest daremne jutro mam kolokwium, jednak jak by siedziec do 3 w
nocy czy jakoś tak to hmm .
4 zad

15 sty 20:32
Hugo: Df:
ex =/= 0
x e R
15 sty 20:36
Hugo: brak asymptot pionowych !
as ukośne
| | 1 | |
lim x−> +−oo f(x)/x = lim... |
| |
| | ex | |
dwa przypadki

dla
| | 1 | |
lim x−> −oo |
| = [e oo  ] = oo |
| | ex | |
15 sty 20:40
john2: tak
15 sty 20:41
john2: jak coś to ja mogę robić wszystkie ( o ile będę umiał ), bo też chcę poćwiczyć to
15 sty 20:43
Hugo: | | x | |
dla b = lim x−> + oo f(x) − ax = |
| = [oo/oo] = H = |
| | ex | |
| | ex −xex | | 1−x | |
lim x−> + oo |
| = lim x−> + oo |
| = −oo |
| | e2x | | e2 | |
15 sty 20:47
Hugo: to prosze jak masz ino ochotę to rób u siebie i mnie kontroluj : ))
ale powiedz mi dla asymptot pionowych wyszlo nam dwa:
oo oraz 0
zatem tą nieskończoność odrzucamy


nie wiem co z nią zrobić
15 sty 20:49
john2: | | 1 | |
po regule masz po prostu |
| |
| | ex | |
15 sty 20:49
john2: a = 0, b = 0
równanie asymptoty poziom y = 0 przy x − > + ∞
15 sty 20:50
Hugo: | | x | |
b = lim x−> −oo |
| =[ −oo * eoo = −oo] |
| | ex | |
zatem nie istnieje ani pionowa ani ukośna asymptota
15 sty 20:51
john2: nie musisz liczyc b przy − nieskonczonosci, jak nie wyszlo a
15 sty 20:54
Hugo: ale jak ;−;
okej dla a jedno wyszlo zero ale drugie dla b?
dla nieskończoności to [oo/oo] symbol nie oznaczoności jak zrobilem HOSPITALEM to wyszlo −oo
//20:47
mozesz mi to wyjasnic? ;c
15 sty 20:55
Hugo: mógłbyś rozpisać b?
15 sty 20:57
john2: chwila zw
15 sty 20:59
Hugo: ja prld Hospitalem zrobilem calosc a nie osobno licznik i mianownik
15 sty 21:02
Hugo: | x | | 1 | |
| = |
| = 0 masz racje |
| ex | | ex | |

dla cb
15 sty 21:02
Hugo:
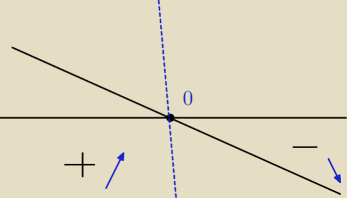
pochodna
0 = e
x(1−x)
e
x = 0 v x = 1
sprzecznosc prawda

e
x =/= 0 wiec tylko x = 1
15 sty 21:09
john2: zwroc uwage, za pomijalismy punkty przeciecia z osiami
to tez wypada robic (o ile sie da)
15 sty 21:10
john2: tak
15 sty 21:10
Hugo: x = 1 a nie 0 −,−
15 sty 21:11
Hugo: wiem wiem na etrapezie TEZ SIE Z NIEgo uCZE

tam sie to robi ale u mnie nie każe
15 sty 21:12
Hugo: f(x) ros .. f(x) mal ...
| | 1 | |
ekstremum minimalne w pkt (1, |
| ) |
| | e | |
i teraz y''=...
15 sty 21:15
Hugo: | | [ex −(ex+xex)]e2x − (ex−xex) *2ex*ex | |
y'' = |
| |
| | e4e | |
powiedz ze dobrze
15 sty 21:23
john2: niepotrzebnie tyle komplikacji
skróciłem z e
x, mianownik i tak jest dodatni
| | −ex − (1−x)ex | |
y''= |
| = teraz zaś skróć |
| | e2x | |
15 sty 21:26
Hugo: tam sie dosc fajnie łączy licznik
| −3e2x(ex+xex) + e3x | | e2x(−2ex−3xex) | |
| = |
| =  |
| e4x | | e4x | |
| −2ex−3xex | | −ex(2+3x) | |
| = |
| |
| e2 | | e2 | |
15 sty 21:31
Hugo: kurde troche inne mamy
15 sty 21:32
john2: | | −1 − (1 −x) | | −1 − 1 + x | | x − 2 | |
... = |
| = |
| = |
| = |
| | ex | | ex | | ex | |
15 sty 21:33
Hugo: czemu masz dalej w liczniku e
x
skoro skróciłeś
15 sty 21:35
Hugo: masz racje...
15 sty 21:35
Hugo: przepisze sb połowe mojego i reszte twojego za pozwoleniem ;x
15 sty 21:36
Hugo:
w kontekście twojego:
e
x jest dodatnie więc
x−2 = 0
x=2
15 sty 21:39
john2: ok
15 sty 21:53
Hugo: xddd widze ze oboje wymiękamy

?
15 sty 22:04
john2: nie, ja ciągle czekam
15 sty 22:07
john2: trochę się męczę z 6) ale raczej się uda
15 sty 22:08
Hugo: w8

15 sty 22:08
Hugo: kyrtap mi zrobil 6

! 5 tez mam
15 sty 22:09
Hugo: Tam ci chyba gdzies pisalem a jak nie to przepraszam
siadam do 7 : ) jak bede juz lulać to przepisze tamte
15 sty 22:09
john2: pisałeś, ale i tak chcę zrobić
15 sty 22:11
Hugo:
Df: (x+1)
2 =/= 0
x e R
15 sty 22:12
john2: x ≠ −1
15 sty 22:13
john2: wskazówka do pochodnej,
jak najszybciej wyciągnij przed nawias wyrażenie (x−1)(x+1)
15 sty 22:19
Hugo: ok

brak pionowych as.
ukośne:
lim x−>+−oo f(x)/x
| | (x−1)2 | | 1 | |
lim x−>+−oo |
| = (wyciągnięcie x2 przed nawias w pamięci) = [ |
| ] = 0 |
| | x(x+1)2 | | oo | |
| | (x−1)2 | | 2x−2 | |
b = lim x−> +− |
| = H = lim x−>+−oo |
| = 1 |
| | (x+1)2 | | 2x+2 | |
y = 1
15 sty 22:19
Hugo: racja −______− przeciez by sie z zerowalo
wiec xe R/{−1}
15 sty 22:20
Hugo: ale jak w pochodnych xd wyciągnąć? stałe sie wyciąga
15 sty 22:22
john2: ok, ale nie trzeba regułą b
15 sty 22:24
Hugo: skoro x =/= −1 to liczymy pionowe
15 sty 22:25
john2: | | 2(x−1)(x+1)2 −(x−1)2*2(x+1) | |
y' = |
| = |
| | (x+1)4 | |
| | (x−1)(x+1) [2(x+1) −(x−1)*2] | |
= |
| = |
| | (x+1)4 | |
15 sty 22:26
Hugo: 
tak spekulowałem ze da sie wyciągnąć przed nawias
15 sty 22:26
john2: przed liczeniem y'' skróć z mianownikiem (x+1)
15 sty 22:31
Hugo: | | (x−1)2 | |
lim x−>−1− |
| = +oo |
| | (x+1)2 | |
| | (x−1)2 | |
lim x−>−1+ |
| = +oo |
| | x+1)2 | |
dobrze mysle? obydwie +oo
15 sty 22:33
Hugo: straszysz

15 sty 22:34
john2: ok
15 sty 22:34
Hugo: | | (x−1)2]' * (x+1)2 − (x−1)2* (x+1)2]' | |
y' = |
| |
| | (x+1)4 | |
| (2x−2)(x+1)2 −(x−1)2 * (2x+2) | |
| |
| (x+1)4 | |
masz jakis pomysl to to wymnazac
15 sty 22:40
john2: patrz na post z 22:26
15 sty 22:41
Hugo: <333333333333333

x2
15 sty 22:42
Hugo: za fajnie wychodzi?
| 2(x+1) [ (x−1)(x+1) − (x+1)(x−1)] | |
| |
| (x+1)4 | |
15 sty 22:49
Hugo: | 2(x+1) [ (x−1)(x+1) − (x−1)(x−1)] | |
| *** tamto źle |
| (x+1)4 | |
15 sty 22:50
john2: jeszcze (x−1) wyciągnij
15 sty 22:51
Hugo: | 4(x−1) | |
| cos da sie jeszcze z tym? |
| (x+1)3 | |
15 sty 22:53
john2: Nie skracaj tego (x+1) dopóki nie zbadasz znaku pochodnej,
dopiero jak zaczniejsz liczyć drugą to skróć
15 sty 22:54
Hugo:
w sumie bz sensu skracac (x+1) bo potem przy przyrównywaniu.....
4(x−1)(x+1) = 0
x = 1 v x = −1
15 sty 22:55
Hugo: bez skracania liczyc drugą? bedzie wiecej roboty ;x ale ok
15 sty 22:56
Hugo: extremum dla x = 1 bo to drugie do dziedziny nie łapie
ekstrema minimalna w pkt (1,0)
f(1) = 0
15 sty 22:58
john2: Jeszcze raz:
Do zbadania pierwszej pochodnej przyda nam się licznik o parzystym stopniu, bo jest zawsze
dodatni. Wtedy badamy znak tylko licznika.
Potem przed zabraniem się do liczenia drugiej pochodnej, skróć to.
15 sty 22:58
john2: dobrze
15 sty 22:59
john2: POPRAWIAM : przyda nam się mianownik o parzystym stopniu
15 sty 23:00
Hugo: | | 4(x−1)(x+1) | |
zatem II pochodna z y' = |
| |
| | (x+1)4 | |
| | 4(x+1)3(x+1)2 | |
= bez skracania = y'' = |
| = 4(x+1) |
| | (x+1)4 | |
x+1 = 0
x= −1 XDDDD tyle liczenia by to nie moglo nalezec do dziedziny
15 sty 23:08
Hugo: no tak bo jak jest mianownik i sie go pozbyt to przez ujemną nie pomnożymy
| | x+3 | |
0 = |
| / * x NIE WOLNO |
| | x | |
15 sty 23:09
Hugo: powiedz mi czy dobrze y'' bo bym wklepal na kartke zrobil tabelke, przepisal 5) i 6) i lulu
:((
15 sty 23:10
john2: | | x−1 | |
y'' = ( 4 * |
| )' = |
| | (x+1)3 | |
| | (x+1)3 − (x−1) * 3(x+1)2 | |
= 4 * |
| = |
| | (x+1)6 | |
| | (x+1)2 [(x+1) − (x−1) * 3] | |
= 4 * |
| = |
| | (x+1)6 | |
| | (x+1) − (x−1) * 3 | |
= 4 * |
| = tutaj skróciłem, bo i tak mam parzysty stopień na dole |
| | (x+1)4 | |
15 sty 23:12
Hugo: zaufam twoim obliczeniom

15 sty 23:17
Hugo: przepisywanie poczeka; tabelka
15 sty 23:25
Hugo:
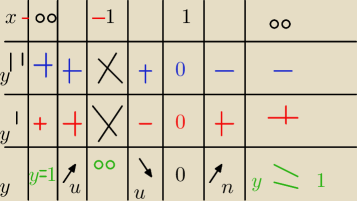
dobrze?
15 sty 23:33
john2: zapomniałeś jeszcze o dwójce
y'' nie ma wartości 0 dla x = 1
dopisz MIN tam gdzie jest wartość minimum lokalnego
przy okazji, jeśli chodzi o
f(x) = x − 2arctgx to to pan z e−trapezu robił, jeśli masz dostęp do kursu
15 sty 23:36
Hugo: ale te argumenty sie podstawialo do głównej funkcji a nie do y'' ;−;?!
| | (1+x)2 | |
f(1) = |
| licznik sie zeruje |
| | (x−1)2 | |
minimum lokalne czyli dla zera

O mam dostęp

15 sty 23:42
Hugo: a skąd dwojka ;−;

15 sty 23:43
john2: tak
chodzi o to, że w pierwszym wierszu napisałeś, że w x = 1
y'' wynosi 0
to nie jest prawdą
y'' jest tam +
15 sty 23:44
john2: 2 to rozwiązanie drugiej pochodnej
15 sty 23:45
16 sty 00:08
john2: ok, nie ma za co, zaraz jeszcze rozpiszę Ci 9, bo już zacząłem
16 sty 00:10
john2: y = ln(sinx),
ale nie jestem tego pewien, zwłaszcza tych granic
dziedzina: x∊(2kπ,π + 2kπ)
granice na krańcach
lim
x−>(2kπ)+ ln(sinx) = [ ln(sin(2kπ)) = ln(0)] = −
∞
lim
x−>(π + 2kπ)− ln(sinx) = [ ln(sin(π + 2kπ)) = ln(0)] = −
∞
Nie umiem obliczyć tych granic od asymtot ukośnych, ale wolfram mówi, że ich nie ma.
| | 1 | |
y' = |
| * cosx = ctgx |
| | sinx | |
dziedzina x∊R\{kπ}
ctgx = 0
ctgx > 0
ctgx < 0
trzeba jeszcze zrobić część wspólną tych wyników z dziedziną naszej funkcji, na dole to
zrobiłem.
zawsze
Wnioski:
Asymptoty poziome:
prawostronna w x =2kπ
lewostronna w x = π + 2kπ
| | π | |
Więc mamy maksimum w punkcie x = |
| + kπ |
| | 2 | |
| | π | | π | |
f( |
| + kπ) = ln( sin( |
| + kπ) = ln1 = 0 |
| | 2 | | 2 | |
| | π | |
Funkcja rośnie x ∊ (2kπ, |
| + 2kπ) |
| | 2 | |
| | π | |
Funkcja maleje ( |
| + 2kπ, π + 2kπ) |
| | 2 | |
Funkcja jest ∩ w całej dziedzinie.
Brak punktów przegięcia.
Ale nie pytaj mnie, jak narysować tabelę, choć może to jest proste
16 sty 00:25
john2: Poprawka: 1 wniosek asymptoty pionowe
16 sty 00:31
Hugo: John

bo myslalem ze tego nie ruszymy xd i juz nie poprawalem
tam jes y=ln|sinx| ...mialem w zeszycie ne czytelnie i nie wiedzialem do konca ale mi
powiedzieli

no nic wielkie dzieki : ) rano jeszcze etrapeza przepisze
16 sty 00:41
Hugo: ahoj

16 sty 07:20
16 sty 07:41
Hugo: Błagam o pomoc
Badanie przebiegu zmienności funkcji y=ln|sinx|
16 sty 08:34
Hugo: moze bedzie dst trzymajcie kciuki

16 sty 09:10
daras: mierny ci wystarczy

16 sty 11:11
 y = y= x −ln(x+1)
D: x> −1
lim x−> −1+ x −ln(x+1) = oo
[−1 − log(−oo) = oo
y = y= x −ln(x+1)
D: x> −1
lim x−> −1+ x −ln(x+1) = oo
[−1 − log(−oo) = oo  ]
zatem istnieje asymptota pionowa prawostronna dla x = −1
]
zatem istnieje asymptota pionowa prawostronna dla x = −1
 ? b jest nie określone
Dziedzina nam wyklucza −oo
[−(ln(oo) ) = − oo]
? b jest nie określone
Dziedzina nam wyklucza −oo
[−(ln(oo) ) = − oo]

 ekstrema:
ekstrema:
 y' = 0
y' = 0
 nie wiem cieszmy sie
nie wiem cieszmy sie  Prosze mnie sprawdzać
Prosze mnie sprawdzać 



 !
z asymptotą ukośną mi tam coś 'b' nie wychodzi
!
z asymptotą ukośną mi tam coś 'b' nie wychodzi ktos moze?
ktos moze?
 john2
'a' źle mam chyba
john2
'a' źle mam chyba
 ?
?




 Dziedzina to x e (−1 ; oo) zatem
−1
0 (z liczenia asymptot jako rozwiaanie)
oo
?
Dziedzina to x e (−1 ; oo) zatem
−1
0 (z liczenia asymptot jako rozwiaanie)
oo
?


 2. czemu masz na odwrót strzałki? funkcja y' przy iksie ma znak minus zatem rysujemy od dolu
zatem musi byc po mojemu?
2. czemu masz na odwrót strzałki? funkcja y' przy iksie ma znak minus zatem rysujemy od dolu
zatem musi byc po mojemu?
 zaskoczyles mnie znowu # y''
ale ta pochodnna y'?
y= x −ln(x+1)
zaskoczyles mnie znowu # y''
ale ta pochodnna y'?
y= x −ln(x+1)


 wychodzi
wychodzi 

 x = 0 v lnx = 0
x = 0 v x = e
f(x) maleje xe (0; e)
f(x) rośnie xe( e; oo)
extremum minimalne dla x = e w punktcie (e, e− )
x = 0 v lnx = 0
x = 0 v x = e
f(x) maleje xe (0; e)
f(x) rośnie xe( e; oo)
extremum minimalne dla x = e w punktcie (e, e− )
 lnx = 1
x = e
przed przekształceniem mamy znak minus przed lnx wiec:
lnx = 1
x = e
przed przekształceniem mamy znak minus przed lnx wiec:
 mamy loga
mamy loga
 rosnąca
co do y'' mam nadzieje ze dobrze policzylem
0 = −x + 2x * lnx
rosnąca
co do y'' mam nadzieje ze dobrze policzylem
0 = −x + 2x * lnx

 jak dla mnie 2xlog bedzie większy od −3x przez co znak przy jest wazny
jak dla mnie 2xlog bedzie większy od −3x przez co znak przy jest wazny
 ?
?
 ?
?
 !
y // −oo // ↗n // p.przeg(...) // ↗ u // 0
!
y // −oo // ↗n // p.przeg(...) // ↗ u // 0
 2/10 zadan
2/10 zadan 




 !
f(x) rosnie xe (0;2 ) U (2; oo)
f(x) maleje xe (−oo; −2) U (−2
!
f(x) rosnie xe (0;2 ) U (2; oo)
f(x) maleje xe (−oo; −2) U (−2 o)
ekstrema minimalna w pkt (0,0)
o)
ekstrema minimalna w pkt (0,0)

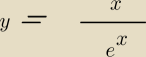 : )))
: )))


 x przy najwyższej ujemny
x przy najwyższej ujemny
 !
!
 nie wiem co dac dla y
nie wiem co dac dla y mam wrazene ze tam źle
mam wrazene ze tam źle

 !
oczywiście ślepe przepisywanie jest daremne jutro mam kolokwium, jednak jak by siedziec do 3 w
nocy czy jakoś tak to hmm .
4 zad
!
oczywiście ślepe przepisywanie jest daremne jutro mam kolokwium, jednak jak by siedziec do 3 w
nocy czy jakoś tak to hmm .
4 zad 
 dla
dla
 ] = oo
] = oo 
 nie wiem co z nią zrobić
nie wiem co z nią zrobić
 dla cb
dla cb
 pochodna
pochodna
 ex =/= 0 wiec tylko x = 1
ex =/= 0 wiec tylko x = 1
 tam sie to robi ale u mnie nie każe
tam sie to robi ale u mnie nie każe

 skoro skróciłeś
skoro skróciłeś
 w kontekście twojego:
w kontekście twojego:
 ?
?

 ! 5 tez mam
! 5 tez mam
 brak pionowych as.
ukośne:
lim x−>+−oo f(x)/x
brak pionowych as.
ukośne:
lim x−>+−oo f(x)/x
 tak spekulowałem ze da sie wyciągnąć przed nawias
tak spekulowałem ze da sie wyciągnąć przed nawias

 x2
x2
 w sumie bz sensu skracac (x+1) bo potem przy przyrównywaniu.....
4(x−1)(x+1) = 0
x = 1 v x = −1
w sumie bz sensu skracac (x+1) bo potem przy przyrównywaniu.....
4(x−1)(x+1) = 0
x = 1 v x = −1

 dobrze?
dobrze?
 O mam dostęp
O mam dostęp 




 jesteś świetnym nauczycielem
jesteś świetnym nauczycielem  przepisalem 5, teraz bede 6 a potem lookne do etrapeza
zycze milej nocki
przepisalem 5, teraz bede 6 a potem lookne do etrapeza
zycze milej nocki 
 bo myslalem ze tego nie ruszymy xd i juz nie poprawalem
tam jes y=ln|sinx| ...mialem w zeszycie ne czytelnie i nie wiedzialem do konca ale mi
powiedzieli
bo myslalem ze tego nie ruszymy xd i juz nie poprawalem
tam jes y=ln|sinx| ...mialem w zeszycie ne czytelnie i nie wiedzialem do konca ale mi
powiedzieli  no nic wielkie dzieki : ) rano jeszcze etrapeza przepisze
no nic wielkie dzieki : ) rano jeszcze etrapeza przepisze

 Badanie przebiegu zmienności funkcji y=ln|sinx|
Badanie przebiegu zmienności funkcji y=ln|sinx|

