zbiór jednoelementowy
MASEŁKO: Dobry wieczór, proszę o pomoc w zadaniu ze zbiorami punktów
Dane są zbiory : A={(x,y) x2 + y2 ≤ 2y}, B = {(x,y) y + x ≥ a} Dla jakich wartości a∊R zbiór
A∩B jest jednoelementowy?
doszedłem do momentu że wyznaczylem rownanie okręgu
x2+(y−1)2≤1
i prostej
y≥−x+a
i teraz nie wiem jak wyznaczyć to a...
wiem że ta prosta i ten okrąg powinny być albo styczne albo przecinające się. narysowałem sobie
wykres (taki roboczy) i wychodzi mi że a powinno się równać <−,0,5,2,5>... niestety nie mam
pomysłu jak to uzasadnić.
14 sty 21:37
MASEŁKO: Nikt nie pomoże? :<
14 sty 21:55
MASEŁKO: up
14 sty 22:13
daras: masełka mi zabrakło i musze smarowac majonezem:(
14 sty 22:16
MASEŁKO: serio nie znajdę tu pomocy? dzięki super forum ;<
14 sty 22:19
daras: tylko kilku wariatów tańczących hobbystycznie z gamoniami
14 sty 22:23
daras: wybacz
14 sty 22:23
MASEŁKO: szkoda jednak że wśród tego waszego tańca z gwiazdami nie znajdzie się nikt kto by zamiast
sobie kpić by nakierował....

14 sty 22:40
daras: bo to taniec śmierci
15 sty 09:09
Dżepetto 18: Panie daras; "Kończ Waść wstydu oszczędź" nabiera wśród Twoich słów nowej interpretacji.
15 sty 09:13
Gray:
 MASEŁKO
MASEŁKO, widziałeś kiedyś okrąg (na płaszczyźnie!), który ma tylko jeden punkt wspólny z
prostą, która nie jest jego styczną?
Prosta y=−x+a musi być styczna do okręgu x
2+(y−1)
2=1. Innymi słowy, układ równań
y=−x+a
x
2+(y−1)
2=1
musi mieć dokładnie jedno rozwiązanie.
Ponieważ x=a−y, to
x
2+(y−1)
2 = (a−y)
2 + (y−1)
2 = 2y
2 − (2a + 2)y + a
2 +1 =1 ⇔
⇔2y
2 − (2a + 2)y + a
2 =0
Δ = (2a + 2)
2 − 8a
2 = −4a
2 + 8a+4 = −4(a−1)
2 +8 = −4((a−1)
2−2) = −4(a−1−
√2)(a−1+
√2),
skąd
a=1+
√2 lub a=1−
√2
Z treści wynika, że należy wybrać a=1+
√2 (dla a=1−
√2 A∩B=A)
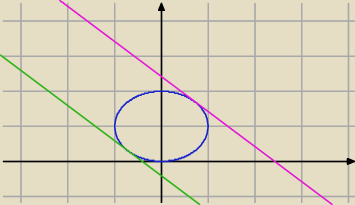
Zobacz rysunek: różowa prosta to ta z właściwie wybranym współczynnikim (kolor na cześć
Milaej Kobi
Ety). Zbiór B, to wszystko nad prostą różową.
15 sty 09:41

 MASEŁKO, widziałeś kiedyś okrąg (na płaszczyźnie!), który ma tylko jeden punkt wspólny z
prostą, która nie jest jego styczną?
Prosta y=−x+a musi być styczna do okręgu x2+(y−1)2=1. Innymi słowy, układ równań
y=−x+a
x2+(y−1)2=1
musi mieć dokładnie jedno rozwiązanie.
Ponieważ x=a−y, to
x2+(y−1)2 = (a−y)2 + (y−1)2 = 2y2 − (2a + 2)y + a2 +1 =1 ⇔
⇔2y2 − (2a + 2)y + a2 =0
Δ = (2a + 2)2 − 8a2 = −4a2 + 8a+4 = −4(a−1)2 +8 = −4((a−1)2−2) = −4(a−1−√2)(a−1+√2),
skąd
a=1+√2 lub a=1−√2
Z treści wynika, że należy wybrać a=1+√2 (dla a=1−√2 A∩B=A)
Zobacz rysunek: różowa prosta to ta z właściwie wybranym współczynnikim (kolor na cześć
Milaej KobiEty). Zbiór B, to wszystko nad prostą różową.
MASEŁKO, widziałeś kiedyś okrąg (na płaszczyźnie!), który ma tylko jeden punkt wspólny z
prostą, która nie jest jego styczną?
Prosta y=−x+a musi być styczna do okręgu x2+(y−1)2=1. Innymi słowy, układ równań
y=−x+a
x2+(y−1)2=1
musi mieć dokładnie jedno rozwiązanie.
Ponieważ x=a−y, to
x2+(y−1)2 = (a−y)2 + (y−1)2 = 2y2 − (2a + 2)y + a2 +1 =1 ⇔
⇔2y2 − (2a + 2)y + a2 =0
Δ = (2a + 2)2 − 8a2 = −4a2 + 8a+4 = −4(a−1)2 +8 = −4((a−1)2−2) = −4(a−1−√2)(a−1+√2),
skąd
a=1+√2 lub a=1−√2
Z treści wynika, że należy wybrać a=1+√2 (dla a=1−√2 A∩B=A)
Zobacz rysunek: różowa prosta to ta z właściwie wybranym współczynnikim (kolor na cześć
Milaej KobiEty). Zbiór B, to wszystko nad prostą różową.