
| 4+3 | ||
równanie prostej AC : y= aAC(x−xC)+yC , aAC= | = 7 | |
| 2−1 |
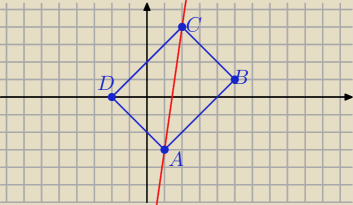



 , C
l: −x−y+b , h: −x−y+b1 . C=(2 ,4) , h: −2−4+b1=0 , b1=6 ,h :−x−y+6 ,znajduję punkt
B
C∊h i C∊d, x −4=−x+6 ,2x=10 ,x=5 ,y=5−4, B=(5,1), wektor AB=[4,4] ,AB=[5−x,1−y], 5−x=4
,x=1
1−y=4, y=−3 ,A=(1, −3) .Prosta ∊AC ;y=ax+b , 2a+b=4 ROZWIĄZUJĘ TEN UKŁAD RÓWNAŃ
a+b=3
równanie prostej zawierającej AC:y=7x−10
, C
l: −x−y+b , h: −x−y+b1 . C=(2 ,4) , h: −2−4+b1=0 , b1=6 ,h :−x−y+6 ,znajduję punkt
B
C∊h i C∊d, x −4=−x+6 ,2x=10 ,x=5 ,y=5−4, B=(5,1), wektor AB=[4,4] ,AB=[5−x,1−y], 5−x=4
,x=1
1−y=4, y=−3 ,A=(1, −3) .Prosta ∊AC ;y=ax+b , 2a+b=4 ROZWIĄZUJĘ TEN UKŁAD RÓWNAŃ
a+b=3
równanie prostej zawierającej AC:y=7x−10
