Badanie przebiegu funkcji Smaug: Witam. Mam funkcję y=x+ln(x)/x z którą mam problem. Mam policzoną dziedzinę x>0, granicę x−>+∞ wynoszącą +∞ oraz x−>0+ wynoszącą −∞. Z pierwszej pochodnej wychodzi mi że funkcja jest cały czas rosnąca, a z drugiej że w przedziale (0; e³/2) jest wklęsła a powyżej e⁽3/2) wypukła. Obliczyłem także asymptotę ukośną x=y i tu pojawia się mój problem, gdyż wychodzi mi że wykres przecina tą asymptotę w p(1,1) i nie pasuje mi też wypukłość tej funkcji. Mógłby mi ktoś pomóc znaleźć mój błąd? Czy wykres może przeciąć tą asymptotę i dążyć do niej ,,ponad" nią?

Janek191: Wszystko jest dobrze Funkcja f najpierw jest wklęsła( pod prostą y = x), a później wypukła ( nad prostą y = x) − orientacyjnie. Trzeba jeszcze dokładnie policzyć punkt przegięcia. Na wykresie tej funkcji wszystko widać

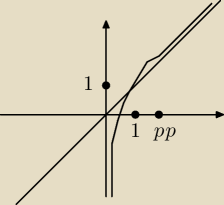
Smaug: @Janek191 Dzięki za odpowiedź. pp wynosi x=e⁽3/2). Próbowałem w wolframie czy googlu narysować ją, ale nie widzę dokładnie tego zachowania, może ona tak wyglądać? (oczywiście pomijając moje umiejętności rysownicze). Jeżeli tak, to od czego zależy czy funkcja może przeciąć asymptotę ukośną czy nie?