Kąt między prostymi
Frost: Proste x+2y=0 i 29x+2y+56=0 są styczne do okręgu ( wzór okręgu nie istotny)
Wyznacz kąt między ostry jaki wyznaczają te styczne.
W odpowiedziach jest 66 stopni a mi za cholerę (przepraszam) nie chce wyjść 66 stopni
cały czas wychodzi mi 60.
liczyłem na 3 sposoby.
ze wzoru na tgα dla prostych przecinających się kiedy proste są w równaniu kierunkowym
a także kiedy są w ogólnym.
i jeszcze na sinα wektorów prostopadłych do nich. Wychodzi nadal 60 stopni

czemu? Błąd w
odp?
13 sty 11:22
Janek191:
x + 2y = 0 ⇒ 2y = − x ⇒ y = − 0,5 x
29 x + 2y + 56 = 0 ⇒ 2y = − 29 x − 56 ⇒ y = −14,5 x − 28
więc a
1 = − 0,5 i a
2 = − 14,5
zatem
| | − 0,5 − ( −14,5) | |
tg φ = I |
| I = |
| | 1 + ( −0,5)*( − 14,5) | |
| | 14 | | 14 | |
= I |
| I = |
| = 1,6969 |
| | 1 + 7,25 | | 8,25 | |
więc
φ ≈ 59
o 30 '
13 sty 11:38
Janek191:
x + 2y = 0 ⇒ 2y = − x ⇒ y = − 0,5 x
29 x + 2y + 56 = 0 ⇒ 2y = − 29 x − 56 ⇒ y = −14,5 x − 28
więc a
1 = − 0,5 i a
2 = − 14,5
zatem
| | − 0,5 − ( −14,5) | |
tg φ = I |
| I = |
| | 1 + ( −0,5)*( − 14,5) | |
| | 14 | | 14 | |
= I |
| I = |
| = 1,6969 |
| | 1 + 7,25 | | 8,25 | |
więc
φ ≈ 59
o 30 '
13 sty 11:38
Janek191:
Zatem jest błąd w odpowiedzi

13 sty 11:39
Frost: Okey dzięki. Ta geometria analityczna wprowadza mnie w szał

wczoraj przez 4 godziny zrobiłem
8 zadań z powtórzenia dzisiaj biorę się za reszte bo jutro sprawdzian. Dzisiaj lepiej bo już
piąte zadanie robię ale w nim brakuje mi jednej rzeczy.
Treść:
W zbiorze wszystkich okręgów stycznych zewnętrznie do okręgu o równaniu x
2+y
2=25
i stycznych jednocześnie do prostej k: 3x−4y −50=0 istnieje okrąg o najmniejszym promieniu.
Wyznacz jego równanie.
mam dwie zależności. odległość środków to suma promieni i odległość środka szukanego
okręgu od prostej k jest równa promieniowi r2.
S(a,b)
wychodzi mi :
a
2+b
2= (r+5)
2
|3a−4b−50|=5r
r− promien szukanego okręgu.
Brak mi trzeciej zależności. Próbuje zapisać zależność między prostymi.
Pamiętam, że na lekcji robiłem przy tablicy to zadanie. Robiłem 45 minut i nic nie
wykombinowaliśmy z nauczycielką

13 sty 11:49
Frost:
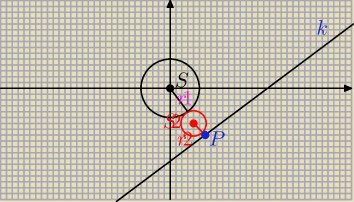
Nie jest tak, że prosta przechodząca przez punkt S1(środek danego okręgu) i P ( punkt
styczności
okręgu szukanego z prostą) leżą na jednej prostej?
S(0,0)
r1=5
k: y= 0,75x−12,5
Musze obliczyć okrąg styczny do prostej k i do okręgu o środku S gdy promień
r2 jest najmniejszy.
13 sty 12:17
Frost: |S1S2|=r1+r2
d(S2,k)=r2
tyle wiem.
13 sty 12:20
Janek191:
Środki tych okręgów leżą na prostej prostopadłej do danej prostej.
Oblicz odległość S1 od tej prostej,d, a następnie 2 r2 = d − r1
13 sty 12:24
J:
r2 będzie najmniejszy, gdy prosta przechodząca przez środki okręgów będzie prostopadła do
danej prostej ...
13 sty 12:26
Frost: Tak żem czuł
Dzięki

13 sty 12:28
Janek191:
Mając równanie prostej prostopadłej wyznacz współrzędne punktu S2 leżącego
na tej prostej korzystając z tego, że jego odległość od prostej stycznej jest równa r2.
S2 = ( x; y)
13 sty 12:30
Frost: Okey, wyszły 2 punkty ale sprawdziłem który to punkt z zależności |S1S2|= r1+r2.
Takie pytanie: jak zrobić indeks dolny ? np r1?
13 sty 12:46
Janek191:
Popatrz na : wpisz a otrzymasz ( III wiersz od góry )

13 sty 12:47
Frost: Dzięki

13 sty 12:48
Frost: Zostało 10 zadań z powtórzenia. W sumie teraz każdy dzień wygląda tak samo:
wracam ze szkoły i zadania z analitycznej i prawdopodobieństwa. 3 tygodnie mam na podszkolenie
się bo 1 lutego AGH.

13 sty 12:50
Janek191:
Dlaczego od I lutego ?
13 sty 12:58
Frost: I lutego jest II etap o diamentowy indeks AGH z matematyki

13 sty 13:14
Janek191:
Myślałem,że studia się zaczynają

13 sty 13:33
Frost: W tym roku matura.
Kolejne zadanko:
Wyznacz współrzędne punktu P równoodległego od punktów A(−9;2) B(3,8) oraz prostej
k: 2x−y−4=0.
Wiem, że będą 2 odpowiedzi. Wyznaczyłem równanie prostej na której leżą punkty P1 P2.
Nie wiem jak powiązać to z trzecią daną czyli odległością punktów P od prostej k.
13 sty 13:39
Janek191:
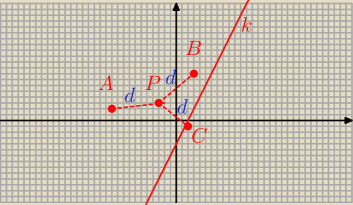
Musi być : I PA I = I PB I = d , gdzie d − odległość P od danej prostej

13 sty 13:49
Janek191:
P = (xo; yo)
13 sty 13:51
Frost: Okey. Zrobione

13 sty 14:00
Janek191:
Jaki jest wynik ?
13 sty 14:07
Frost: P
1=(−3,5)

13 sty 14:09
 czemu? Błąd w
odp?
czemu? Błąd w
odp?

 wczoraj przez 4 godziny zrobiłem
8 zadań z powtórzenia dzisiaj biorę się za reszte bo jutro sprawdzian. Dzisiaj lepiej bo już
piąte zadanie robię ale w nim brakuje mi jednej rzeczy.
Treść:
W zbiorze wszystkich okręgów stycznych zewnętrznie do okręgu o równaniu x2+y2=25
i stycznych jednocześnie do prostej k: 3x−4y −50=0 istnieje okrąg o najmniejszym promieniu.
Wyznacz jego równanie.
mam dwie zależności. odległość środków to suma promieni i odległość środka szukanego
okręgu od prostej k jest równa promieniowi r2.
S(a,b)
wychodzi mi :
a2+b2= (r+5)2
|3a−4b−50|=5r
r− promien szukanego okręgu.
Brak mi trzeciej zależności. Próbuje zapisać zależność między prostymi.
Pamiętam, że na lekcji robiłem przy tablicy to zadanie. Robiłem 45 minut i nic nie
wykombinowaliśmy z nauczycielką
wczoraj przez 4 godziny zrobiłem
8 zadań z powtórzenia dzisiaj biorę się za reszte bo jutro sprawdzian. Dzisiaj lepiej bo już
piąte zadanie robię ale w nim brakuje mi jednej rzeczy.
Treść:
W zbiorze wszystkich okręgów stycznych zewnętrznie do okręgu o równaniu x2+y2=25
i stycznych jednocześnie do prostej k: 3x−4y −50=0 istnieje okrąg o najmniejszym promieniu.
Wyznacz jego równanie.
mam dwie zależności. odległość środków to suma promieni i odległość środka szukanego
okręgu od prostej k jest równa promieniowi r2.
S(a,b)
wychodzi mi :
a2+b2= (r+5)2
|3a−4b−50|=5r
r− promien szukanego okręgu.
Brak mi trzeciej zależności. Próbuje zapisać zależność między prostymi.
Pamiętam, że na lekcji robiłem przy tablicy to zadanie. Robiłem 45 minut i nic nie
wykombinowaliśmy z nauczycielką 
 Nie jest tak, że prosta przechodząca przez punkt S1(środek danego okręgu) i P ( punkt
styczności
okręgu szukanego z prostą) leżą na jednej prostej?
S(0,0)
r1=5
k: y= 0,75x−12,5
Musze obliczyć okrąg styczny do prostej k i do okręgu o środku S gdy promień
r2 jest najmniejszy.
Nie jest tak, że prosta przechodząca przez punkt S1(środek danego okręgu) i P ( punkt
styczności
okręgu szukanego z prostą) leżą na jednej prostej?
S(0,0)
r1=5
k: y= 0,75x−12,5
Musze obliczyć okrąg styczny do prostej k i do okręgu o środku S gdy promień
r2 jest najmniejszy.






 Musi być : I PA I = I PB I = d , gdzie d − odległość P od danej prostej
Musi być : I PA I = I PB I = d , gdzie d − odległość P od danej prostej 

