Opisik Darek: Wyznacz wartości parametru m, dla których zbiorem rozwiązań danej nierówności jest przedział (−2;0).

2
	>m
x+2

pigor: ... wychodzi mi m=−1... może być

pigor: ..., przepraszam m=1 .

Darek: może być tylko jak Pan to zrobil ?

pigor: ..., widzę to np. tak:

2
	>m /* (x+2)2 i (*)x≠−2⇒ 2(x+2) >m(x+2)2 ⇔
x+2

⇔ m(x+2)²−2(x+2)< 0 ⇔ (x+2)[m(x+2)−2]< 0 i x∊(−2;0) ⇔ ⇔ m(x+2)−2= x ⇔ m(x+2)−2−x= 0 ⇔ m(x+2)−1(x+2)= 0 ⇔ ⇔ (x+2)(m−1)= 0 , stąd i z (*) ⇒ m=1 . ...

Darek: Ciężko mi zrozumieć co się z czego bierze

Darek: Wytłumaczyłby mi to ktoś?

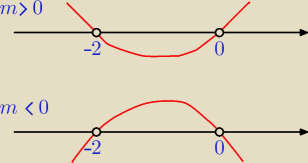
Bogdan: Proponuję takie rozwiązanie:

	2		mx + 2m − 2		2   m(x + 2 − )   m
m −		< 0 ⇒		< 0 ⇒		< 0
	x + 2		x + 2		x + 2

Przechodzimy do nierówności równoważnej:

	2		2
m(x + 2 −		)(x + 2) < 0, x1 = −2 +		, x2 = −2
	m		m

x∊(−2, 0), przypadek m < 0 nie zachodzi.

	2
−2 +		= 0 ⇒ m = ...
	m