Maturka Mesj: Witam. Jak graficznie rozwiązywać nierówności....? Przykład : |^2x−2_x−4|>4

Eve:

2x−2		2x−2
	>4 i		<−4
x−4		x−4

Mesj: To akurat wiem. Nie wiem co robić dalej.

5-latek: Jesli wiez to dlaczego nie napisales ?

Mesj:

	6		6
Mogę napisać żaden problem. Teraz:		+2>4 i		+2<−4 Poprawnie? Co dalej?
	x−4		x−4

5-latek:

	2x−2
np		>4 dla x≠4
	x−4

mnozymy obie strony nierownosci przez kwadrat mianownika(wiemy wtedy ze nie mnozymy przez liczbe ujemna (2x−2)(x−4)>4(x²−4) dalej Ty Tak samo rozwiaz druga nierownosc

Mesj: x²−11x+28>0 i co teraz mam to narysować?

5-latek: Pokaze CI jak rozwiazywac takie nierownosci

	a		|a|
Znasz zapewne taka wlasnosc wartosci bezwzglednej |		|=
	b		|b|

Wiec nasza nierownosci wyjswciowa rozpiszmy tak

|2x−2|
	>4 dla x nie rowna sie 4
|x−4|

Poniewaz dla xnie rowna sie 4 |x−4| jest zawszae dodatnia to mozemy obie strony nierownosci pomnozyc przez |x−4| i dostaniemy |2x−2|>4|x−4| a takie nierownosci to juz potrafisz rozwiazywac (czyli przedzialy i jedziesz

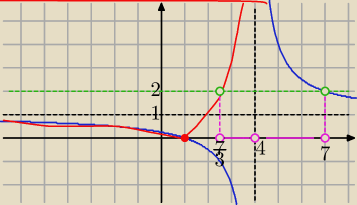
Eta: Miało być graficznie x≠4

	x−1		3
2|		|>4 ⇒ [f(x)]]= 1+
	x−4		x−4

g(x)= |f(x)| i h(x)=2

|x−1|
	= 2 ⇒ |x−1|=2|x−4| ⇒ x−1=2x−8 v x−1= −2x+8
|x−4|

x= 7 v x= ⁷₃

	7
odp : x∊(		, 4) U (4,7)
	3

Eta: Ta niebieska część hiperboli po prawej nad osią ma być czerwona

Mesj: Bardzo dziękuję

Eta: Widzisz błąd ? x= 7 v x−1=−2x+8 ⇒ 3x=9 ⇒ x=3 popraw odp: ............