Wariacje, permutacje, kombinatoryka Martiminiano: Dobry wieczór, mam prośbę o pomoc z kilkoma zadaniami z wariacji, permutacji i kombinatoryki 1. Ze zbioru {1, 2, 3, .... , 100} losujemy kolejno bez zwracania dwie liczby. Oznaczamy je w kolejności losowania n i k. Ile jest takich wyników losowania, w których n+k=111? Wiem, że są to pary {11,100} {12,99} itd., ale jak to poprawnie zapisać nie robiąc tego "na piechotę"? 2. Ze zbioru {1, 2, 3, ...., 50} losujemy kolejno ze zwracaniem dwie liczby. Oznaczamy je w kolejności losowania n i k. Ile jest takich wyników losowania, w których |n−k|≤2 ? Tu z kolei wiadomo, że będą to możliwości gdy wylosujemy tę samą liczbę, sąsiadujące, albo różne o 2. Ale pojawia się ten sam problem co wyżej. 3. Ze zbioru {1, 2, 3, ...., 10} losujemy kolejno bez zwracania trzy liczby. Oznaczamy je w kolejności losowania a, b, c. Ile jest takich wyników losowania, w których a+b+c=21? 4. Z talii 24 kart (od dziewiątki do asa w każdym z 4 kolorów) losujemy 5 kart. Na ile sposobów możemy wylosować karty, by znalazły się wśród nich 3 karty tej samej wartości i 2 karty innej

	4 3		20 2
wartości (np. 3 asy i 2 dziesiątki)? Tu z kolei moim zadaniem jest to		*		, ale w

podręczniku w odpowiedziach jest, że możliwości jest 720, a nie 760... Wszelkie uwagi i wskazówki mile widziane, niekoniecznie rozwiązania

Martiminiano: Zapomniałem o jeszcze jednym, ile jest liczb dziewięciocyfrowych, których suma cyfr jest równa 3? Sam w tym czasie cały czas próbuję rozwiązać te zadania, gdyby się jednak udało, to poinformuję

Mila: 21:43 mozesz obliczyć rozważając sumy:

	8!
1+2+0+0+0+0+0+0+0 − mozliwości		=8permutacje z powtórzeniami
	7!

	8!
2+1+0+0+0+0+0+0+0 −mozliwości		=8 permutacje z powtórzeniami
	7!

3+0+0+0+0+0+0+0+0 jedna liczba

	8!
1+1+1+0+0+0+0+0+0		= 28
	2!*6!

Razem 8+8+1+28=45 II sposób (x₁+1)+x₂+x₃+...+x₉=3 pierwsza cyfra różna od zera ⇔x₁+x₂+x₃+...+x₉=2 Szukana liczba rozwiązań tego równania w zbiorze N. Korzystamy z wzoru: (kombinacje z powtórzeniami) n=2 k=9

2+9−1 9−1		10 8		10 2		1
	=		=		=		*10*9=45
						2

Martiminiano: Dziękuję. Kombinacje z powtórzeniami, niestety w podręczniku nie mam żadnych informacji o tym. Jak wygląda wzór ogólny?

Eta:

	n!
Pn(k1, k2, k3)=		, k1, k2, k3 .... powtórzenia elementów
	k1!*k2!*k3!

Mila: Kombinacje z powtórzeniami − matematyka dyskretna, tylko na zajęciach koła mat. w LO. Wzór :

n+k−1 k−1

Martiminiano: Dziękuję bardzo

Mila: Zadanie 4. Myślę tak: Masz 6 kategorii w kartach: 9,10,W,D,K,A W każdej kategorii 4 karty. Losujemy 5 kart:

6 1		4 3		5 1		4 2
	*		*		*		=6*4*5*6

Wybór kategorii i z niej 3 karty. Następnie wybór jednej kategorii z 5 pozostałych i wybór 2 kart z tej kategorii. W ten sposób wylosujemy np. układ (A♠,A♥,A♦,9♣,9♦) Gdyby te dwie karty miały być różne to byłoby inaczej.

Martiminiano: Właśnie nie mogłem zrozumieć tego w poleceniu, czy to mają być np. 99, JJ, QQ, czy dwie różne karty. Dziękuję bardzo

Mila: Napisz odpowiedzi do pozostałych zadań, z jakiego to zbioru?

Eta: Karty zawsze są różne

Mila: Tak, ale chodziło o wartości np. 9pik,9karo. Zadanie niejasno sformułowane.

Martiminiano: Po prostu z podręcznika "Prosto do matury 3" zakres podstawowy i rozszerzony. 1. 90 2. 244 3. 42

Mila: 1) {1,2,3,4,5,6,7,8,9,10,11,....100} 11+100=111 Od 11 do 100 mamy 90 liczb, które możemy połączyć w 45 par dających sumę 111. Każda para na 2 sposoby: (11,100),(100,11) itd Razem: 90 Pozostałe jutro. (Jeśli będzie potrzeba) Dobranoc.

Martiminiano: Jeśli uda mi się zrobić, to napiszę. W innym razie dalej będę zainteresowany pomocą. Dziękuję bardzo! Dobranoc.

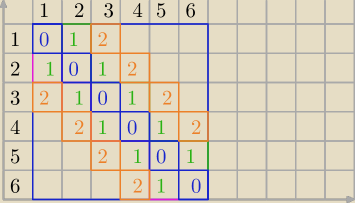
Mila: 2) uogólniając: Liczba par (n,k) gdzie |n−k|≤2 jest równa : n+2*(n−1)+2*(n−2) Dla n=50 50+2*49+2*48=50+98+96=244

Martiminiano: Dziękuję bardzo Teraz się rozjaśniło