geometria analityczna-okręgi i proste dipsi: Wyznacz równanie okręgu o promieniu 5, który jest styczny do osi OY i jednocześnie styczny do prostej k: 3x+4y−6=0

Eve: do równania okręgu raz wstawiasz x=0 a raz x =.... z równania prostej szukasz p i q

dipsi: można to napisać, bo nie rozumiem

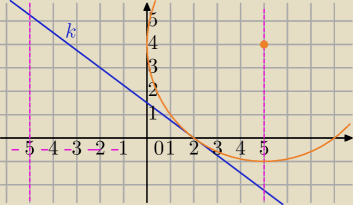
Mila: k: 3x+4y−6=0⇔ 4y=−3x+6

	−3		3
k: y=		x+
	4		2

Promień jest prostopadły do OY⇔środek okręgu leży na prostej x=5 albo x=−5 S(5,y) S(−5,y) odległość S od prostej K jest równa 5 1)

	|3*5+4y−6|
5=		⇔
	√32+42

|15+4y−6|=25 |4y+9|=25 4y+9=25 lub 4y+9=−25 4y=16 lub 4y=−34

	−17
y=4 lub y=
	2

	−17
S1=(5,4) lub S2=(5,		)
	2

Następny okag w drugim wpisie

Mila: S₁=(5,4) Równanie: (x−5)²+(y−4)²=25

	−17
S2=(5,		)
	2

	17
(x−5)2+(y+		)2=25
	2

Pozostałe dwa środki okręgów wyznacz z równania

	|3*(−5)+4y−6|
5=
	√32+42

Dokończ