Nierówności trygonometryczne Mistrz: Rozwiąż nierówność: cosx−sinx<0 Prosiłbym o pomoc, ponieważ nie bardzo co mam z tym zrobić. Dodam, że takich nierówności typu cos2x itp. nie przerabialiśmy na lekcji.

Eve: ale tam nie ma cos2x?

Mistrz: Nie ma, tak jak napisałem cosx−sinx<0. To, że takich przykładów nie robiliśmy dodałem można powiedzieć jako ciekawostke

Eve: przenieś sin na prawo, zastąp cos z jedynki i podnieś do kwadratu, zapisz założenia

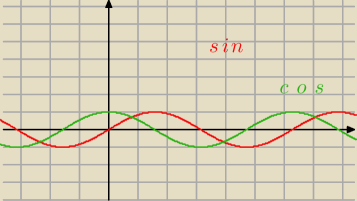
Hugo: cosx < sinx narysuj sobie i odpowiedz sb na fundamentalne pytanie, kiedy to zachodzi

Bogdan: a może tak:

	π		π		π		π
cosx − sinx = sin(		− x) − sinx = 2sin(		− x) cos		= √2sin(		− x)
	2		4		4		4

	π		π		π
√2sin(		− x) < 0 ⇒ sin(		− x) < 0 ⇒ sin[−(x −		)] < 0
	4		4		4

	π		π
− sin(x −		) < 0 ⇒ sin(x −		) > 0
	4		4

Hugo: z wykresu łatwiej, widać ze dla pi/4 do pi/2 + pi/4 jest większy a okresowość wynosi 2kpi

Mistrz: Bogdan w sumie właśnie dlatego dodałem tą ciekawostkę, że podobnych przykładów nie robiliśmy mógłby mi ktoś powiedzieć jeszcze jaki wyjdzie wynik w przedziale x∊<0,2π>? Wtedy bym już wiedział całkiem o co chodzi

Mistrz: Wyszłoby x∊(pi/4 +2kpi , 5/4pi +2kpi ) jeśli się nie mylę tak ?