geometria analityczna Frost: w okrag o srodku (6,4) wpisano trójkąt równoboczny ABC którego jednym z wierzchołków jest punkt A (2,6). Oblicz współrzędne pozostałych wierzchołków. mam obliczony wektor AS czyli promień, mam obliczony punkt S2 ( 8,3) S2 jest środkiem wektora CB więc mam zależność współrzędnych xb od xc i yb od yc. wektor AC też mam obliczony. ale nadal nie wiem jak obliczyć chociaż jeden punkt. z równań na długości np. wektora AC nie mogę obliczyć punktu C. Myślałem nad wzorem na sin60 między wektorami AB i AC ale to też nie wystarczy. Czekam na podpowiedzi

Frost: Trudne? Wiem

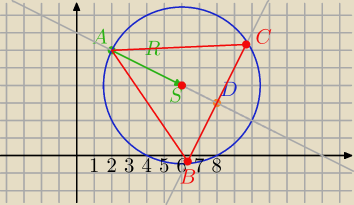
Mila: S=(6,4), A=(2,6) AS^→[4,−2] D− środek BC

	1
SD→=		AS→=[2,−1]
	2

S(6,4)→T_[2,−1]→D=(6+2,4−1)=(8,3) prosta AS:

	1
y=−		x+7
	2

Prosta AC: AC⊥AD a: y=2x+b i D∊a Dokończ

Frost: Napisałaś, że prosta AC ⊥ AD a to nieprawda, pr BC⊥ AD pr BC ma wzór y=2x−13 jeśli dobrze obliczyłem.

Frost: podstawiając wzór prostej BC do wzoru okręgu dostanę dwa rozwiązania. czyli jedną ze współrzędnych punktów B i C. racja?

Frost: Wyszło mi równanie kwadratowe ale Δ<0 czyli jakby nie miał ten okrąg żadnych punktów wspólnych z prostą BC

Mila: Tak, to literówka, jak widać z rysunku. BC⊥AD Prosta dobrze BC: y=2x−13 (x−6)²+(y−4)⁴=20 y=2x−13 (x−6)²+(2x−17)²=20 x=8−√3 lub x=8+√3 y=3−2√3 lub y=3+3√3

Frost: Tak samo miałem zapisaną nierówność. Wkurzony jestem na siebie bo pomysł dobry miałem jak zawsze tylko rachunki.. i przez to siedzę godzine nad zadaniem które robi się w 10 minut

Mila: Tak to bywa, nie ma się co złościc. Powodzenia.