Ostatnie zadanie
5-latek:
 Milu
Milu pamietasz moze to cwiczenie nr 58 (o tych nierownosciach trojkata )
Tam dostalismy taka nierownosc |a+b|≤|a|+|b|
Mam zastosowac to cwiczenie do zadania nr 106 do saprawdzenia czy podane rownania maja
rozwiazania .
Jak to wyglada na osi
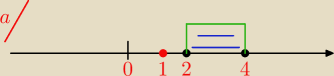
a) |x−2|+|4−x|=1
Poniewaz suma odleglosci liczby 2 i 4 wynosi 2 a ma wynosic 1 wiewc to rownanie nie ma
rozwiazn
A jak to sprwdzic na podstawie tego cwiczenia ?
11 sty 20:54
Mila:
|x−2|+|4−x|≥|x−2+4−x|=2
11 sty 20:58
Mila:

Suma odległości od 2 i 4 na osi dla dowolnego x∊<2,4> jest większa od 1.
Jeżeli yweźmiemy spoza przedziału <2,4> tym bardziej suma odległości y od 2 i 4 jest wieksza od
1.
11 sty 21:05
5-latek: czyli z tego wnioskuje tak ze
|x−2|=1 i |4−x|=1
czyli mozemy zapisac ze
|(x−2)+(4−x)|<=|x−2|+|4−x|=2
Za chwile napiszse drugie rownanie i poproszse Cie o sprawdzenie
11 sty 21:06
5-latek: b) |x−2|+|x−4|=1 (chyba sie pomylili bo to przeciez to samo co w przykladzie a)wyjdzie
11 sty 21:10
Mila:
źle21:06
11 sty 21:11
Mila:
Ale musisz to wykazac z 21:10.
11 sty 21:12
5-latek: Musimy na osi zaznaczyc punkty 2 i 4 (bo bierzemy ze zmienionym znakiem
11 sty 21:13
5-latek: czemu 21:06 zle ?
Zrobilem to wedlug tego przepisu co jest w ksiazce
11 sty 21:16
5-latek: Moze chodzi o to <= ? zapisalem tak ten znak ≤
Jak piszse te znaki z gory to potem mi sie to wszysko zlewa w 1 linijke
11 sty 21:20
5-latek:
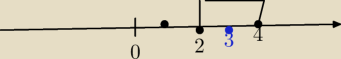
b) |x−2|+|4−x|≥|x−2+4−x|=2
Tam w cwiczeniu jest wskazowka ze mozna skorzytac z wlasnosci ktora dzisiaj udowadnialem dlugo
ze |x|=|−x|
Zaraz wstawie ostatnie rownanie
11 sty 21:26
Lorak: Z 21:06 wniosek, że |x−2|=1 i |4−x|=1 był niedobry. Dalej ok.
11 sty 21:33
Mila: 21:26 dobrze.
11 sty 21:34
5-latek:
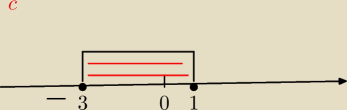
c) |x+3|+|x−1|=3
Na osi wychodzi ze rownanie to nie ma rozwiazan gdyz suma dleglosci od −3 i 1 dla dowolnego x
<∊−3,1> jest wieksza od 3
|x+3|+|1−x| ≥|x+3+1−x|=4
Dziekuje bardzo z asprawdzenie i za okazana pomoc

11 sty 21:37
Mila:

11 sty 21:39
5-latek: Milu 
Twoja pomoc jest naprawde nieoceniona w pozytywnym znaczeniu i powiem tak niewyceniona
Wobec tego caly

11 sty 21:47
 Milu pamietasz moze to cwiczenie nr 58 (o tych nierownosciach trojkata )
Tam dostalismy taka nierownosc |a+b|≤|a|+|b|
Mam zastosowac to cwiczenie do zadania nr 106 do saprawdzenia czy podane rownania maja
rozwiazania .
Jak to wyglada na osi
a) |x−2|+|4−x|=1
Poniewaz suma odleglosci liczby 2 i 4 wynosi 2 a ma wynosic 1 wiewc to rownanie nie ma
rozwiazn
A jak to sprwdzic na podstawie tego cwiczenia ?
Milu pamietasz moze to cwiczenie nr 58 (o tych nierownosciach trojkata )
Tam dostalismy taka nierownosc |a+b|≤|a|+|b|
Mam zastosowac to cwiczenie do zadania nr 106 do saprawdzenia czy podane rownania maja
rozwiazania .
Jak to wyglada na osi
a) |x−2|+|4−x|=1
Poniewaz suma odleglosci liczby 2 i 4 wynosi 2 a ma wynosic 1 wiewc to rownanie nie ma
rozwiazn
A jak to sprwdzic na podstawie tego cwiczenia ?
 Suma odległości od 2 i 4 na osi dla dowolnego x∊<2,4> jest większa od 1.
Jeżeli yweźmiemy spoza przedziału <2,4> tym bardziej suma odległości y od 2 i 4 jest wieksza od
1.
Suma odległości od 2 i 4 na osi dla dowolnego x∊<2,4> jest większa od 1.
Jeżeli yweźmiemy spoza przedziału <2,4> tym bardziej suma odległości y od 2 i 4 jest wieksza od
1.
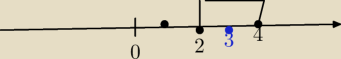 b) |x−2|+|4−x|≥|x−2+4−x|=2
Tam w cwiczeniu jest wskazowka ze mozna skorzytac z wlasnosci ktora dzisiaj udowadnialem dlugo
ze |x|=|−x|
Zaraz wstawie ostatnie rownanie
b) |x−2|+|4−x|≥|x−2+4−x|=2
Tam w cwiczeniu jest wskazowka ze mozna skorzytac z wlasnosci ktora dzisiaj udowadnialem dlugo
ze |x|=|−x|
Zaraz wstawie ostatnie rownanie
 c) |x+3|+|x−1|=3
Na osi wychodzi ze rownanie to nie ma rozwiazan gdyz suma dleglosci od −3 i 1 dla dowolnego x
<∊−3,1> jest wieksza od 3
|x+3|+|1−x| ≥|x+3+1−x|=4
Dziekuje bardzo z asprawdzenie i za okazana pomoc
c) |x+3|+|x−1|=3
Na osi wychodzi ze rownanie to nie ma rozwiazan gdyz suma dleglosci od −3 i 1 dla dowolnego x
<∊−3,1> jest wieksza od 3
|x+3|+|1−x| ≥|x+3+1−x|=4
Dziekuje bardzo z asprawdzenie i za okazana pomoc 

 Twoja pomoc jest naprawde nieoceniona w pozytywnym znaczeniu i powiem tak niewyceniona
Wobec tego caly
Twoja pomoc jest naprawde nieoceniona w pozytywnym znaczeniu i powiem tak niewyceniona
Wobec tego caly 