:))
Blue: zad.1 Dany jest sześcian ABCDA1B1C1D1. Wyznacz cosinus kąta między prostymi DM i BD1.
11 sty 20:51
Mila:
Co to M?
11 sty 21:14
Eta:
M?
11 sty 21:18
Blue: Przepraszam, jakaś rozkojarzona jestem
M to środek krawędzi AA1
11 sty 22:05
Mila:
Tw. Pitagorasa , potem tw. cosinusów.
|BD1|=a√3
11 sty 22:47
Blue: Mila, ale ja nie rozumiem, o jaki kąt chodzi...
11 sty 23:04
Mila:
Te proste są skośne, źle wcześniej przeczytałam.Przeczytałam BM.
Myślę, że możesz sobie darować to zadanie. A jaka jest odpowiedź?
11 sty 23:17
11 sty 23:26
Mila:
Jak przemyślę dobrze, to napiszę jutro.
Może wcześniej narysuje Bogdan albo Tadeusz.
11 sty 23:30
11 sty 23:34
Bogdan:
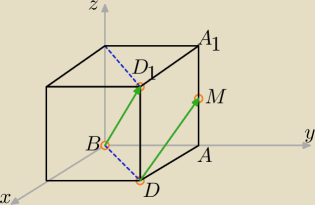
Proponuję skorzystać z narzędzi geometrii analitycznej w przestrzeni (takie ujęcie nie
znajduje się w programie nauczania szkoły średniej, a szkoda).
Przyjmuję długość krawędzi sześcianu 2a.
B = (0, 0, 0), A = (0, 2a, o), M = (0, 2a, a), D = (2a. 2a, 0), D
1 = (2a, 2a, 2a)
Wyznaczam współrzędne wektorów:
→ →
BD
1 = [2a, 2a, 2a], DM = [−2a, 0, a]
Iloczyn skalarny tych wektorów (pomijam znak →)
BD
1◯DM = |BD
1|*|DM|*cosα =
√4a2+4a2+4a2*
√4a2 + 0 + a2*cosα = 2a
2√15 cosα
oraz
BD
1◯DM = 2a*(−2a) + 2a*0 + 2a*a = −2a
2
| | 1 | | √15 | |
2a2√15 cosα = −2a2 ⇒ cosα = − |
| = − |
| |
| | √15 | | 15 | |
12 sty 00:25
Kacper:
Bardzo fajne zadanie, tylko ciekawe jakie rozwiązanie proponuje autor zadania.
Ja osobiście mam pewien pomysł ale potrzebuje czasu na wykonanie rysunku
12 sty 08:44
Mila:
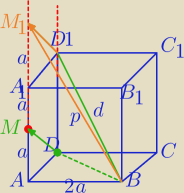
Pierwsza myśl u mnie też taka. W LO jednak nie ma geometrii analitycznej w R3.
Kąt między prostymi skośnymi to kąt między ich wektorami równoległymi ( informacja dla
Blue)
W moim rozwiązaniu wychodzi mi dodatnia wartość cosinusa.
Spójrzcie Panowie.
DM
→||D1M1
→
12 sty 15:16
Kacper:
Zerknę w piątek
12 sty 16:24
Blue: Chyba odpuszczę sobie to zdanie
12 sty 18:30
Mila:
Jeden raz widziałam na maturze odległość między skośnymi przekątnymi sześcianu.
Jednak z mojego rysunku łatwo obliczysz cos kąta.
MD został przesunięty równolegle do punktu D1.
12 sty 18:34
Blue: Mila, a jaka to była matura?
12 sty 21:55
Eta:
maj 2015
12 sty 21:59
Blue: Jasne
Apropo maturki, mam wyniki z rozszerzenia, za wiele się nie pomyliłam − 68%
12 sty 22:01
Mila:
1994 rok .
12 sty 22:03
Mila:
To bardzo ładny wynik, gratuluję.
12 sty 22:03
Eta:
w maju ma być 100% ( to dostaniesz więcej jabłek)
12 sty 22:05
Blue: taa 100% chyba z podstawy ^^ (chociaż w sumie w to też wątpię)
Mila, tak dawno, nawet na świecie mnie nie było
12 sty 22:06
franco: Mila:
Mamy trójkąt BM1D1. Po wyliczeniu niestety cos tego kąta jest dodatni. Może Milo zobacz
14 mar 07:00
Kacper:
| | √15 | |
Tak sobie pomyślałem, że a∊(0,90) i cosα= |
| . |
| | 15 | |
Teraz kąt 180−α jest kątem rozwartym między tymi prostymi − a wiadomo, że cos(180−α)=−cosα,
| | −√15 | |
czyli cos(180−α)= |
| |
| | 15 | |
Zatem, w zależności od uznawanej przez nas definicji kąta między prostymi oba wyniki są ok
Mnie zawsze uczyli, że wybieramy nie większy z nich
14 mar 12:41
franco: Myślenie ma przyszłość. Dzięki za wyjaśnienie
15 mar 05:49