Rownanie bezwzgledne . 5-latek: Rozwiaz geometrycznie rownanie |x−1|+|x−3|=2 Nie chodzi mi o rozwiazanie na przedzialach bo to potrafie Chodzi mi czy jest jakis inny sposob aby to szybciej rozwiazc (z odleglosci punktow Podejrzalem na woframie i tam jest takie rozwiazania 1≤x≤3

5-latek: Kiedys to tlumaczyl pigor ale nie ma tego niestety

bezendu:

5-latek: Czesc Radku Chodzi mi bardziej zeby to zrobic bez wykresu

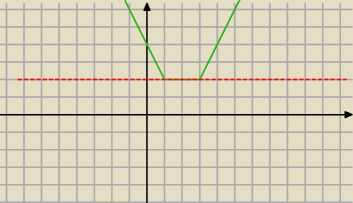
Mila: Równość |x −1 |+ |x−3| = 2 spełniają liczby, których suma odległości od liczb 1 i 3 jest równa 2. Ponieważ odległość liczb 1 i 3 na osi jest równa 2, ten warunek spełniają wszystkie liczby z tego przedziału: <1,3> 1≤x≤3

5-latek: dziekuje CI bardzo za ten rysunek A np taki przyklad (wymyslam |x+5|−|x−3|= −6 Dalem zeby bylo minus a nie plus (mozesz to rozwiazac jesli sie da rozwiazac ?

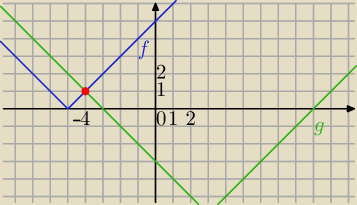
Mila: Np. tak: |x+5|=|x−3|−6 f(x)=|x+5| g(x)=|x−3|−6 x=−4 Spr. L=|−4+5|=1 P=|−4−3|−6=7−6=1 L=p x=−4 ====

5-latek: dziekuje czyli nie wszystkie takie rownania mozna rozwiazac na osi . Czasmi trzeba korzystac z wykresu Dobrze