 Wielomiany
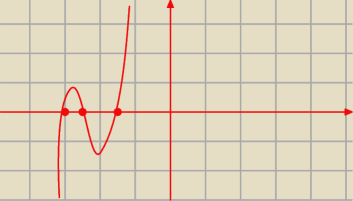
Wielomian trzeciego stopnia f, którego fragment wykresu przedstawiono na rysunku spełnia
warunek f(0)=90 , wiedząc że wielomian g dany jest wzorem g(x)= x3−14x2+63x−90. Wykaż że
g(x)=−f(−x) dla x ∊R
wyszło mi że g(x) = x3+14x2+63x+90 i nie wiem co dalej
Wykres powyżej
Wielomiany
Wielomian trzeciego stopnia f, którego fragment wykresu przedstawiono na rysunku spełnia
warunek f(0)=90 , wiedząc że wielomian g dany jest wzorem g(x)= x3−14x2+63x−90. Wykaż że
g(x)=−f(−x) dla x ∊R
wyszło mi że g(x) = x3+14x2+63x+90 i nie wiem co dalej
Wykres powyżej  Punkty to miejsca zerowe : −3, −5, −6
Punkty to miejsca zerowe : −3, −5, −6
 pomyłka
pomyłka
 nie wiedziałam jak tylko zamienić na −f(−x)
nie wiedziałam jak tylko zamienić na −f(−x) 