trapez w okręgu
Patri:
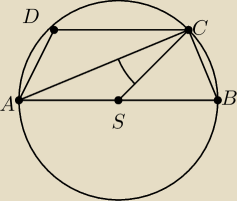
Oblicz miary kątów trapezu równoramiennego ABCD, wiedząc, że kąt ACS ma miarę 38.
Nie mam klarowności w tym zadaniu, zależnie od której strony się zabiorę, dostaję różne wyniki.
Może coś jawnie robię nie tak. Pomożecie?
Kąt zaznaczony na rysunku to ten dany ACS ma 38.
Trojkąt ABC jest prostokątny, więc kąt SCB ma 52. (52+38=90)
Trójkąt SBC jest równoramienny, kat SBC ma też 52 stopnie, (ramiona są promieniami).
Trójkąt ASC jest równoramienny, więc kąt CAS ma 38, a kąt ASC 104.
Kąt DAS też ma 52 bo to trapez równoramienny.
Jak poprowadzę odcinek DS, to dostaję dwa przystające trójkąty SBC i ASD.
(Są przystające, jeśli są lustrzanym odbiciem?
)
Trójkąt DSC jest równoramieny, kąt DSC ma miarę (180−76−76=28) 28 stopni, kąt SCD=kąt CDS i
wynosi (180−28)/2 = 76
76+52=128
Czyli kąty trapezu 52,52, 128, 128.
Albo − okrąg opisany na czworokącie − suma przeciwległych kątów 180.
No i wyszło teraz, a sama to różne dziwactwa dostawałam...
Ommmm.
Dzięki
