wartosci bezwzgledne (rownania )
5-latek: Rozwiaz rownania
a) |x|=−x to x<0
b) |x+1|=x+1 to x ≥−1
c) √4−4x+x2=x−2 to |2−x|= x−2 to 2−x≤0 to −x≤−2 to x≥2
d) √9+6x+x2= x+3 to |3+x|=x+3 i tu mam problem z okresleniem czy
czy wartosc bezwzgledna z liczby 3+x jest liczba przeciwna do x+3
11 sty 13:39
5-latek: |3+x|= 3+x dla x≥0
|3+x|= −(3+x)= −3−x (czyli nie jest do nie liczba przeciwna bo nie dostalismy x+3
Glupieje juz
11 sty 13:50
asdf:
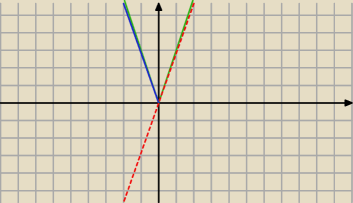
dobrze jest przedstawic takie proste przyklady graficznie. Zobacz, ze wartosc bezwzgledna to
inaczej odleglosc, a takie wartosci nie moga byc ujemnie, czyli:
|f(x)| >0 ∀
x∊D, D = R, np. f(x) = 3x, D = (−
∞,
∞)
|f(x)| = |3x| = 3|x|
jakby sobie narysowac prostą:
y = 3x to masz czerwoną prostą (wykres)
bylo napisane wyzej, ze wartosci nie moga byc ujemne, czyli trzeba rozdzielić tą funkcje na
zbior funkcji:
| ⎧ | f(x), x > 0 | |
| ⎩ | −f(x), x ≤ 0 |
|
=
wiem, ze dla x≤ 0 funkcja jest ujemna bo wystarczy policzyc:
3x ≤ 0, x≤0
itd...jak bedziesz miec funkcje:
3x+3, to tez liczysz te wartosci, zmieniasz znaki itd, prosta sprawa.
11 sty 14:03
asdf: |x+1| = x+1 jest tylko prawdziwe jesli x≥1, bo jak sobie te dwie proste narysujesz to tylko w
przedziale:
x ≥ 1 funkcja:
|x+1| pokrywa sie z x+1
11 sty 14:05
asdf: sorry, x≥−1
11 sty 14:06
5-latek: Dziekuje za wyjasnienie

11 sty 14:09
J:
Cześć
małolat ...:
nic nie trzba rysować ...

z definicji ...IaI = a , gdy a ≥ 0
Ix+1I = x + 1 , gdy x + 1 ≥ 0...

11 sty 14:12
5-latek: czesc
J 
Ten przyklad wlasnie zrobilem z definicji
Nie mialem klopotu z przykladem c) gdyz wartosc bezwzgledna liczby |2−x| jest liczba przeciwna
do x−2
Natomiast mialem duzy klopot z przykladem d)
11 sty 14:19
asdf: jasne, nic nie trzeba rysowac, wyjasniac, bo po co? od razu mozna robic! Na codzien uzywam
matematyki, ale raczej w pisaniu programow, a nie zeby cos policzyc, dlatego inaczej do tego
podchodze, sorry. Mam inne podejscie do matematyki

Sama definicja to nic...chyba lepiej
jest widziec zastosowanie.
11 sty 14:23
asdf: |3+x| = 3 + x, dla x ...Narysuj i zobacz

Jesli cos to pytaj
11 sty 14:25
J:
I3+xI = Ix+3I ... i jasne...

11 sty 14:26
J:
..co więcej ... zauważ, że prawa strona musi być nieujemna ...

11 sty 14:28
5-latek:
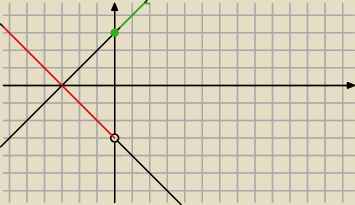
dla x≥0 ten zielony
Natomiast dla x<0 |3+x|= −(3+x)= −3−x jest ten czerwony
11 sty 14:32
5-latek: czyli |x+3|=x+3 to x≥−3
11 sty 14:36
5-latek: Rozwiazania na osi liczbowej to sobie zrobie juz sam w zeszycie .
11 sty 14:38
asdf:
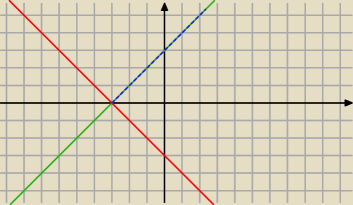
z definicji:
|f(x)| = |3+x| = |3 + x|
f(x) = 3+x , x >= −3
−(3+x), x<3
masz znalezc te same punkty (=) z funkcja: x+3, od razu widac 3+x, geometrycznie:
czerwony:
−(3+x)
zielony:
3+x
niebieski:
3+x
nie trzeba sobie tego wszystkiego rysowac, ale na sam start warto wiedziec jak to sie ma.
Pozniej mozna to olac jak sie zalapie o co w tym chodzi

11 sty 14:41
asdf: zobacz, ze zaznaczylem niebieską półprostą w przedziale (−3,∞), bo wlasnie w tym przedziale
miesci sie zielona, troche to zle rozrysowane, ale pewnie zalapiesz.
11 sty 14:43
5-latek: Dziekuje CI. Teraz zalapalem dokladnie z tymi rysunkami

Caly czas piszse dla x>=0 lub x<0 ze zamiast pisac dla x gdzie zeruje sie modul piszse x>=0 i
x<0

11 sty 14:48
asdf: wartosc bezwzgledna tak jakby ograniczenie zbioru danej funkcji, musisz tak pokombinowac ze
znakiem, zeby nie byl ujemny, czyli tam gdzie wartosci funkcji sa ujemne, musisz zmienic znak,
np.
y = |x
2 − 3| jak sobie policzysz (albo i najlepiej narysujesz) to zobaczysz, ze w −
√3,
√3
są wartości ujemne, czyli trzeba zmienic znak funkcji, dać: −y. a wiec funkcja bedzie taka:
| | ⎧ | y, x>√3 i x<−√3 | |
| |y| = | ⎩ | −y, x w przedziale wyzej napisanym |
|
11 sty 15:04
 dobrze jest przedstawic takie proste przyklady graficznie. Zobacz, ze wartosc bezwzgledna to
inaczej odleglosc, a takie wartosci nie moga byc ujemnie, czyli:
|f(x)| >0 ∀x∊D, D = R, np. f(x) = 3x, D = (−∞,∞)
|f(x)| = |3x| = 3|x|
jakby sobie narysowac prostą:
y = 3x to masz czerwoną prostą (wykres)
bylo napisane wyzej, ze wartosci nie moga byc ujemne, czyli trzeba rozdzielić tą funkcje na
zbior funkcji:
dobrze jest przedstawic takie proste przyklady graficznie. Zobacz, ze wartosc bezwzgledna to
inaczej odleglosc, a takie wartosci nie moga byc ujemnie, czyli:
|f(x)| >0 ∀x∊D, D = R, np. f(x) = 3x, D = (−∞,∞)
|f(x)| = |3x| = 3|x|
jakby sobie narysowac prostą:
y = 3x to masz czerwoną prostą (wykres)
bylo napisane wyzej, ze wartosci nie moga byc ujemne, czyli trzeba rozdzielić tą funkcje na
zbior funkcji:

 z definicji ...IaI = a , gdy a ≥ 0
Ix+1I = x + 1 , gdy x + 1 ≥ 0...
z definicji ...IaI = a , gdy a ≥ 0
Ix+1I = x + 1 , gdy x + 1 ≥ 0...
 Ten przyklad wlasnie zrobilem z definicji
Nie mialem klopotu z przykladem c) gdyz wartosc bezwzgledna liczby |2−x| jest liczba przeciwna
do x−2
Natomiast mialem duzy klopot z przykladem d)
Ten przyklad wlasnie zrobilem z definicji
Nie mialem klopotu z przykladem c) gdyz wartosc bezwzgledna liczby |2−x| jest liczba przeciwna
do x−2
Natomiast mialem duzy klopot z przykladem d)
 Sama definicja to nic...chyba lepiej
jest widziec zastosowanie.
Sama definicja to nic...chyba lepiej
jest widziec zastosowanie.
 Jesli cos to pytaj
Jesli cos to pytaj


 dla x≥0 ten zielony
Natomiast dla x<0 |3+x|= −(3+x)= −3−x jest ten czerwony
dla x≥0 ten zielony
Natomiast dla x<0 |3+x|= −(3+x)= −3−x jest ten czerwony
 z definicji:
|f(x)| = |3+x| = |3 + x|
f(x) = 3+x , x >= −3
−(3+x), x<3
masz znalezc te same punkty (=) z funkcja: x+3, od razu widac 3+x, geometrycznie:
czerwony:
−(3+x)
zielony:
3+x
niebieski:
3+x
nie trzeba sobie tego wszystkiego rysowac, ale na sam start warto wiedziec jak to sie ma.
Pozniej mozna to olac jak sie zalapie o co w tym chodzi
z definicji:
|f(x)| = |3+x| = |3 + x|
f(x) = 3+x , x >= −3
−(3+x), x<3
masz znalezc te same punkty (=) z funkcja: x+3, od razu widac 3+x, geometrycznie:
czerwony:
−(3+x)
zielony:
3+x
niebieski:
3+x
nie trzeba sobie tego wszystkiego rysowac, ale na sam start warto wiedziec jak to sie ma.
Pozniej mozna to olac jak sie zalapie o co w tym chodzi 
 Caly czas piszse dla x>=0 lub x<0 ze zamiast pisac dla x gdzie zeruje sie modul piszse x>=0 i
x<0
Caly czas piszse dla x>=0 lub x<0 ze zamiast pisac dla x gdzie zeruje sie modul piszse x>=0 i
x<0 