wartości parametru a, żeby równanie |x+a|=1-||x-2|-3| miało 2 rozwiązania matek: Dla jakich wartości parametru a równanie |x+a|=1−||x−2|−3| ma dokładnie 2 rozwiązania? Proszę o pomoc (liceum)

J: Wystarczy, aby prawa strona była dodatnia

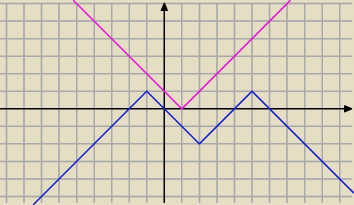
Gray: Rozwiąż to zadanie graficznie. Na niebiesko narysowałem funkcję prawej strony. Powinieneś sam utworzyć taki wykres bez trudu. Wykres lewej strony (różowy dla a=−1) to przesunięcie różowego o −a. O ile można go przesuwać, aby spełnić treść zadania?

matek: hmm.. czyli a bedzie z przedziałów (−2,0) (4,6)?

Gray: Odwrotnie: (−6,−4) ∪ (0,2), bo |x+a| to przesunięcie |x| o wektor [[−a,0].

matek: no tak, fakt. Dzięki za pomoc

aaaaa: βγγδδδδδπ∞∞∞≥∞Δδ∑⇒⇔