planimetria tyu: Mam znów pytanie do zadania o poniższej treści. Obwód trapezu równoramiennego opisanego na okręgu jest równy 16, a przekątna trapezu ma długość 5. Oblicz długość promienia okręgu wpisanego w ten trapez i promienia okręgu opisanego na nim. tutaj jest rozwiązanie http://www.zadania.info/d1411/2433168 Dolna podstawa dzieli się na odcinki: a,

8−a−a
	=4−a
2

Wiem dlaczego dolna podstawa składa się z odcinka długości "a", ale nie wiem, dlaczego te dwa

	8−a−a
boczne odcinki mają długość		=4−a.
	2

Jeszcze nie wiem dlaczego AC`=4

tyu: czy ktoś pomógłby mi z tymi długościami dolnej podstawy, bo podział na podstawie takiej zasady jest w innym zadaniu

Eve: 2a+2b=16⇒a+b=8⇒b=8−a

	a−b		a−(8−a)		a−8+a
x=		=		=		=?
	2		2		2

Eve: AC'=a−4+8−a=4 h z Tw Pitagorasa

tyu: dziękuję. Właśnie wróciłem na forum. Zaraz przeanalizuję to co napisałaś

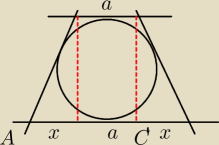
tyu: 2a+2x=8 /:2 a+x=4 x=4−a skoro AC`=x+a oraz x=4−a więc AC`=4−a+a=4 Teraz rozumiem. Dziękuję