g. analityczna. styczna do okregu tomek: napisz równania ogólne stycznych do danego okręgu o i przechodzących przez punkt A jeśli: o: X² + y² +6x +2y +5=0 , A(−2,2) zupełnie nie wiem jakim sposobem znaleźć to równanie, proszę o pomoc

pigor: ..., np. tak : x²+y²+6x+2y+5=0 /+5 i A=(−2,2) ⇒ x²+6x+9+y²+2y+1= 5 ⇔ (x+3)²+(y+1)²= 5 i A=(−2,2), to jeśli (x',y')=? − punkt styczności mamy szukane równanie stycznej (*) (x+3)(x'+3)+(y+1)(y'+1)=5, które dla (x,y)=(−2,2)=A przyjmuje postać x'+3+3y'+3=5 ⇔ x'+3y'= −1 i z równaniem okręgu daje układ : x'= −1−3y' i (x'+3)²+(y'+1)²= 5 z którego obliczysz sobie 2 punkty styczności (x',y') i podstawisz je do (*) otrzymując szukane proste styczne.

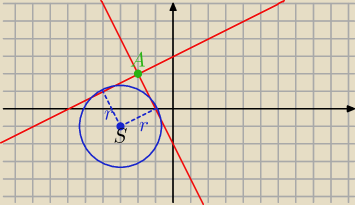
Eta: o:(x+3)²+(y+1)²=5 S(−3, −1) , r= √5 styczna ma równanie: s: y=ax+b i A(−2,2)∊s ⇒ 2=−2a+b ⇒ b= 2a+2 s: y= ax+2a+2 ⇒ ax−y+2a+2=0 odległość punktu S od stycznej jest równa r=√5

	|−3a+1+2a+2|
to		=√5
	√a2+1

|3−a|=√5√a²+1 /² |9−6a+a²|=5a²+5 ⇒ 9−6a+a²=5a²+5 lub 9−6a+a²= −5a²−5 2a²+3a−2=0 lub 3a²−3a+7=0 −−− sprzeczność a=0,5 v a=−2 to b=3 v b= −2 są dwie takie styczne: y= 0,5x+3 v y= −2x−2 w postaci ogólnej: x−2y+6=0 v 2x+y+2=0

tomek: dziękuje Wam bardzo !