Dla jakich wartości parametru m równanie x2+2(m−3)|x|+m2−1=0 ma trzy różne rozwi
Malzy: Dla jakich wartości parametru m równanie x2+2*(m−3)*|x|+m2−1=0 ma trzy różne rozwiązania? Dla
znalezionej wartości parametru m podaj rozwiązania tego równania.
Proszę o odpowiedź, doszedłem tylko do podstawienia t = |x| i równania t2+2*(m−3)*|x|+m2−1=0,
natomiast nie mam pomysłów na warunki dla 3 rozwiązań. Z góry dziękuje za pomoc.
10 sty 23:58
xa:
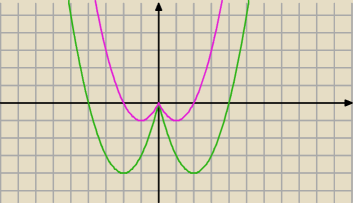
11 sty 00:23
Malzy: No tak, tylko miałem to zrobić bez rysowania wykresów (których i tak pewnie bym nie zrobił, bo
mam tam niewiadomą x i parametr m), algebraicznie.
Przy takich zadaniach robiłem to w ten sposób, że podstawiałem t = |t|, a następnie dobierałem
odpowiednie warunki na deltę i wzory Viete'a. Na 2 i 4 różne rozwiązania jestem w stanie
dobrać warunki, natomiast nie wiem, jakie one będą dla 3 rozwiązań.
Wykres trochę pomógł, ponieważ (jeśli się nie mylę) te warunki powinny wyglądać tak:
Δ > 0 ⋀ t1*t2=0 (jedno rozwiązanie jest zerem) ⋀ t1+t2>0 (drugie rozwiązanie jest rozwiązaniem
dodatnim)... W sumie to chyba już wiem, jak to zrobić. Dzięki za podpowiedź w postaci wykresu.

11 sty 00:52
Gray: Było kilka dni temu.
11 sty 13:30
xa:
−

11 sty 14:03


