Test IV Blue: zad.1 W trójkącie ABC poprowadzono dwusieczną AK. Okrąg wpisany w trójkąt ABK i okrąg opisany na trójkącie ABC są współśrodkowe. Wyznacz miary kątów trójkąta ABC. zad. 2 Udowodnij, że jeśli dla pewnego a∊R liczba 2^a+2^−a = 3, to liczba 4^a+4^−a jest liczbą całkowitą. Ja to zrobiłam tak: 4^a+4^−a = ( 2^a+2^−a)²−2*2^a*2^−a = 3²−2¹*2⁰=9−2=7 Może tak być? Ktoś pomoże z tym 1 zadaniem Może jakiś rysunek?

Mila: 2) dobrze. 1) za chwilę, muszę spojrzeć do kuchni.

Mila: 72,72,36 Taka odpowiedź?

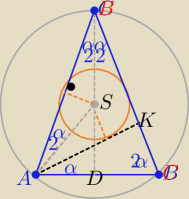
Eta: Taki trójkąt w którym S jest środkiem okręgu wpisanego w trójkąt ABK jest trójkątem równoramiennym, bo środek tych okręgów leży na dwusiecznej kąta ABC i jednocześnie symetralnej BD 5α=180^o ⇒ α=36^o , 2α= 72^o

Blue: Tak, Mila, właśnie taka

Eta: Na początku nie wpisałam,że: ..... wpisanego w trójkąt ABK i środkiem okręgu opisanego na trójkącie ABC

Blue: Dzięki Eta, w życiu sama bym na to nie wpadała