Równania Nataalka: rozwiąż algebraicznie i graficznie |x−y|=2 2x+ y=1 Czy mogę to zrobić metodą podstawiania gdzie y=1−2x ? niestety nie wychodz mi wynik Taki sam provlem z kolejnym przykładem |y−1|=2 x−y=1

Eve: a dlaczego nie wychodzi? 3x−1=2 i 3x−1=−2

pigor: ..., np. takie rozwiązanie algebraiczne : |x−y|=2 i 2x+ y=1 ⇔ (x−y= −2 i 2x+y=1) v (x−y=2 i 2x+y=1) ⇔ ⇔ (3x=−1 i y=x+2) v (3x=3 i y=x−2) ⇔ (x= −¹₃ i y= ⁵₃) v (x=1 i y=−1) ⇔ ⇔ (x,y)=(−¹₃,⁵₃) v (x,y)=(1,−1) − szukane 2 rozwiązania układu. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− rozwiązanie algebraiczne : ... ⇔ (x−y= −2 i 2x+y=1) v (x−y=2 i 2x+y=1) ⇔ ⇔ (y=x+2 i y=−2x+1) v (y=x−2 i y=−2x+1) − rysujesz 3 proste o tych równaniach i współrzędne (x,y) ich punktów przecięcia, to szukane 2 rozwiązania jak wyżej.

pigor: ... , ups, ...oczywiście to drugie − pod kreską −−−−−−−−−−−−−−−−−−−−−−−−− to opis rozwiązania graficznego danego układu równań

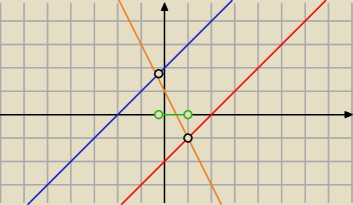
Marcin: Graficznie

pigor: ..., pięknie; no właśnie ; dzięki, tylko niestety − jak zwykle − ani be, ani me najbardziej zainteresowani ...