Ekstremum lokalne funkcji maturzystka: Znaleźć ekstremum funkcji: y=x*pierwiastek 3 stopnia z (1−x²) D=<−1−1>

	1		−2		1
y'=x*		*(1−x2)[		]*(−2x)+(1−x2)[		]
	3		3		3

3
	=x2
5

	√15		√15
x=		lub x=−
	5		5

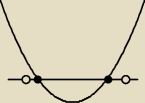
Rysuję funkcję, zaznaczam miejsca zerowe uwzględniam dziedzinę Df'(−1,1)

	√15		√15
w miejscu		mam min lokalne, a w miejscu −		mam max lokalne
	5		5

	2√6
fmin=
	5

	2√6
fmax=−
	5

	−3√3		−1
W odpowiedziach mam tylko minimum równe		w punkcie		....
	16		2

john2: Skąd taka dziedzina?

maturzystka: Pomyliło mi się, miało być y=x*pierwiastek (1−x²)³

maturzystka:

	3
dobra już chyba wiem, zrobię jeszcze raz, tam powinno być
	2

john2: Chyba głupie pytanie zadałem. http://www.wolframalpha.com/input/?i=domain+f%28x%29+%3D+root[x%2C3] myślałem, że dziedzina to R przy nieparzystym stopniu

maturzystka:

	1		1
No ale i tak mi się nie zgadza bo wychodzą 4 miejsca zerowe, 1,−1,−		,		... czyli na
	2		2

wykresie wychodzi dwa minima i maksima...

john2: Jaka w końcu jest postać naszej funkcji? Przy okazji dziedzina ³√x to jednak R, wolfram coś miesza.

john2: f(x) = x√(1−x²)³

maturzystka: ale ta funkcja wygląda tak: http://www.wolframalpha.com/input/?i=y%3Dx*sqt%28%281-x%5E2%29%5E3%29

john2: Ok, zaraz spróbuję.

john2: Nie wiem, kto Ci daje te zadania, ale albo chodzisz do ambitnej szkoły, albo ktoś Cię nie lubi. W każdym razie ma wyjść maksimum w x = 1/2 i minimum w x = −1/2. Nie zawsze musi być extremum tam, gdzie pochodna jest równa zero. x=−1 i x = 1 wg mnie odpadną jako kandydaci na ekstrema, bo są to krańce przedziału, dla których funkcja jest określona. Ekstremum jest wtedy, gdy da się znaleźć obustronne otoczenie danego punktu i wartość funkcji w tym punkcie jest mniejsza (minimum) lub większa (maksimum) od wartości funkcji dla pozostałych argumentów z tego otoczenia. Punkt − 1 nie ma lewostronnego otoczenia, a 1 prawostronnego. Na przykład funkcja f(x) = √x nie ma minimum w x = 0, bo przed 0 nie ma funkcji. Mogę się mylić.

john2: Oczywiście mowa o ekstremach lokalnych.