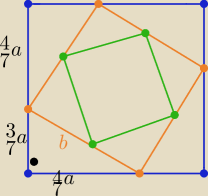
Granica ciągu liczbowego - rozszerzenie jatoja: W kwadrat o boku długości a wpisano drugi kwadrat w ten sposób, że jego wierzchołki leżą na bokach kwadratu poprzedniego i dzielą go na dwie części w stosunku 4:3. W ten drugi kwadrat wpisano analogicznie kwadrat trzeci itd. Oblicz sumę pól wszystkich utworzonych w ten sposób kwadratów. ODPOWIEDŹ: ⁴⁹₂₄a² Proszę o pomoc w rozwiązaniu!

Eta:

	9		16		25
b2=		a2+		a2=		a2
	49		49		49

wartości pól tworzą ciąg geometryczny malejący

	25
S1=a2 , S2=b2=		a2
	49

S₁+S₂+S₃+...... +S_n −−− suma ciągu geometrycznego zbieżnego

	25
|q|<1 bo q=		, a1= a2
	49

	a1		49
S=		= .................. =		a2
	1−q		24