Klasa 3
Ala: Na obozie było 40 uczestników. 30 umiało tylko pływać, 8 grało tylko w tenisa a 3 zarówno
pływało jak i grało w tenisa. Ile osób nie uprawiało żadnego sportu?
10 sty 11:42
Ala: Proszę pomóżcie . Przygotowuje się do konkursu i mam wątpliwości przez jeden wyraz dlatego
wpisałam zadanie do rozwiązania przez tęgie głowy. Może kiedyś też będę pomagała.
10 sty 13:04
hejhejhejehejheeheje: 40−wszyscy
30− pływa
8−tenis
3−pływa i tenis
x− nie uprawia sportu
a więc od tych 30 odejmujemy te 3 osoby i od 8 odejmujemy te 3 osoby
bedzie równanie
27+5+3+x=40
x=5
10 sty 13:11
Ala: A co z tym TYLKO w treści zadania? Przez ten wyraz mam wątpliwości. Bardzo dziękuje za
zainteresowanie.
10 sty 13:14
hejhejhejehejheeheje: chyba ze bd 27+8+3+x=40, i x=2
czyli 27−tylko pływa
8−tylko gra w tenisa
3−pływa i gra
x− nic
10 sty 13:23
PW: P − zbiór osób pływających (i być może grających w tenisa)
T − osoby grające w tenisa (i być może pływające).
Wiadomo, że dla dowolnych zbiorów
(1) |P∪T)| = |P| + |T| − |P∩T|.
Po odjęciu stronami liczby |P∩T| dostajemy:
|P∪T)| − |P∩T| = (|P| − |P∩T|) + (|T| − |P∩T|).
Różnice w nawiasach oznaczają liczbę osób tylko pływających i liczbę osób tylko grających w
tenisa.
Po podstawieniu danych:
|P∪T)| − 3 = 30 + 8
P∪T jest zbiorem osób uprawiających jeden ze sportów,
|P∪T)| = 41.
Wniosek: dane są niespójne (nie ma takiej możliwości).
Widać to zresztą "gołym okiem" − bez żadnych wzorów. Skoro (30+8) = 38 osób uprawia dokładnie
jeden ze sportów, a do tego dochodzą 3 osoby uprawiające obie dziedziny, to sportowców na
obozie jest 38+3 = 41 − więcej niż uczestników, dane są sprzeczne.
Gdyby nie było słów "tylko", to rozwiązanie istniałoby, z zależności (1) wynikałoby, że sport
uprawia
30+8 − 3 = 35 uczestników, a więc 40−35 = 5 uczestników nie uprawia żadnego ze sportów.
10 sty 15:14
Eta:
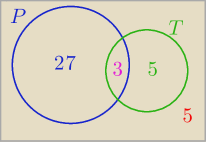
10 sty 15:19
Ala: Dziękuje bardzo
10 sty 15:28
