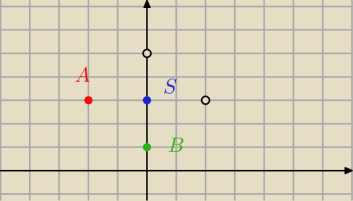
Matura podstawowa Ada: 3. Kwadrat o bokach A(−2,3) B(0,1) ma środek symetrii w punkcie S(0,3) Oblicz: a) współrzędne pozostałych wierzchołków b) pole kwadratu c) stosunek pola kwadratu do pola koła wpisanego w kwadrat. Osią symetrii dla dwóch punktów jest prosta x=0, więc drugi punkt ma współrzędną x z innym znakiem: D(2,3). Dla drugich dwóch punktów osią symetrii jest prosta y = 3. Odległość BS = |3−1| = 2, więc 4 współrzędna to C(0, 4). b) a = √(−2−0)²+(3−1)² = √4+4 = 2√2 P = a² = 8 c)

	1
r =		a = √2
	2

P_k = πr² = 2π≈ 2*3,14 = 6,28

	P		8
n =		=		= 1,27389
	Pk		6,28

5-latek : P_k=2π i tak zostaw (π sie zawszse zostawia w takiej postaci

	P		8		4
n=		=		=
	Pk		2π		π