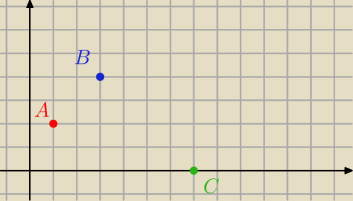
Matura podstawowa Ada: 2. W trapezie ABCD (AB||CD) dane są punkty A(1,2), B(3,4), C(7,0). a) Napisz równanie prostej CD w postaci ogólnej b) Oblicz długość wysokości trapezu prosta AB: 2 = a +b 4 = 3a+b 2−4 = a−3a −2 = −2a ⇒ a = 1 b = 1 y_AB = x+1 postać ogólna: y−x−1 = 0 prosta CD: y = x + b 0 = 7+b ⇒ b=−7 y_CD = x−7 postać ogólna: y−x+7 = 0 b) wysokość h to odległość punktu C od prostej AB

	|(−1)*7+1*0−1|		|−8|		8
h=		=		=		= 4√2
	√(−1)2+(1)2		√2		√2

Eve:

Janek191: a) Inny sposób rozwiązania: C = ( 7 ; 0 ) D = ( x; y) → → CD = AB [ x − 7 ; y − 0 ] = [ 2 ; 2] x − 7 = 2 i y = 2 x = 9 i y = 2 D = ( 9 ; 2) Prosta CD y = a x + b 0 = 7 a + b 2 = 9 a + b −−−−−−−− odejmujemy stronami 2 = 2a ⇒ a = 1 b = − 7 a = − 7*1 = − 7 więc y = x − 7 − postać kierunkowa x − y − 7 = 0 − postać ogólna ==========