Dowody:) Blue:

	4		6
zad.11. Niech A,B ⊂ Ω oraz P(A) =		i P(B) =		. Udowodnij, że prawdopodobieństwo
	7		7

	1		2
warunkowe spełnia nierówność		≤P(A|B)≤		.
	2		3

Coś czuję, że przyczepicie się do takiego rozwiązania, ale cóż, wrzucę: http://i59.tinypic.com/2ezjzmo.jpg

	1
zad.12 Udowodnij, że jeśli a>0, b>0 oraz a + 2b = 1, to ab≤		.
	8

http://i57.tinypic.com/1e2rew.jpg zad.17 Wykaż, że jeśli długości boków trójkąta tworzą ciąg arytmetyczny, to długość promienia

	1
okręgu wpisanego w ten trójkąt jest równa		długości wysokości opuszczonej na średni bok
	3

tego trójkąta. http://i60.tinypic.com/4fv786.jpg Byłabym wdzięczna, gdyby ktoś to sprawdził

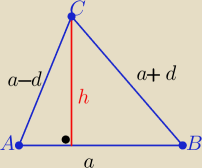Eta: zad.17 d −− różnica ciągu arytmetycznego, d<a a−d, a, a+d −−− długości boków trójkąta tworzące ciąg arytmetyczny a−−− dł. średniego boku h −− dł. wysokości opuszczonej na średni co do długości bok r −−− dł. promienia okręgu wpisanego w ten trójkąt

	2PΔ
r=		, p=a+a−d+a+d= 3a , 2PΔ= a*h
	p

	a*h		1
r=		=		h
	3a		3

c.n.u

Eta: Porównaj czasochłonność rozwiązania tego zadania

Blue: Wiedziałam, że pewnie można zrobić to prościej Ale moje też może być, tak Eta?

Blue: https://matematykaszkolna.pl/forum/273228.html Eta, jakbyś mogła, to zajrzyj jeszcze tutaj

Eta: zad.12 ok

Blue: a co z 11? Udowodnione to jest? Czy jednak nieuznane by to było ?

Mila: Może być. Podam inna propozycję. 1) P(A∪B)=P(A)+P(B)−P(A∩B)≤1⇔

4		6
	+		−P(A∩B)≤1⇔
7		7

10
	−1≤P(A∩B)⇔
7

3
	≤P(A∩B)
7

	6
2)P(A∪B)=P(A)+P(B)−P(A∩B)≥		⇔
	7

10		6
	−		≥P(A∩B)⇔
7		7

	4
P(A∩B)≤
	7

z (1 i 2)

3		4
	≤P(A∩B)≤		/ : P(B)
7		7

3		7		P(A∩B)		4		7
	*		≤		≤		*		⇔
7		6		P(B)		7		6

1		P(A∩B)		2
	≤		≤
2		P(B)		3

Eta: Hej Mila A już miałam prawie to samo pisać .......( tylko nie w pionie, a w linijkach

Mila: Ja lubię przestrzeń. Witaj Eto.

Eta:

Blue: Dziękuję

Kacper: