funkcje wymierne Codę::Blak: zasadnij , że trójkąty ograniczone osiami układu współrzędnych i dowolna prostą majacą jeden punkt wspólny z wykresem funkcji y=1/x(x>0)maja jednakowe pola

Codę::Blak: Up

===: ... mało tego ... to pole zawsze równa się 2 −

===: ... fajne zadanko ... może komuś jeszcze się przyda A swoją drogą coraz częściej pojawia się równanie prostej w postaci odcinkowej ...

	1
Na krzywej obieramy punkt M=(xM,		)
	xM

	1
f'(x)=−
	x2

	1
f'(xM)=−
	xM2

Styczna do krzywej w punkcie M

	1		1		x		2
y−		=−		(x−xM) ⇒		+y=
	xM		xM2		xM2		xM

x		y
	+		=1
2xM		2   xM

	2   2xM*   xM
SΔ=		=2 Jak widać pole to nie zależy od punktu styczności.
	2

PW: Mam pewne wątpliwości. W treści zadania mówią o prostej, która ma jeden punkt wspólny z wykresem. Nie jest wcale oczywiste, że styczna ma jeden punkt wspólny z wykresem. Gdyby funkcja była inna, rozumowanie może być błędne. Wolałbym rozwiązanie bez użycia pochodnej, ale takie, w którym konstruuje się prostą i pokazuje, że ma rzeczywiście tylko jeden punkt wspólny z wykresem.

===: ... gdyby była inna ... Ale przecież to jest konkretne zadanie

PW: Ale nawet nie podjąłeś próby wykazania, że styczna ma tylko jeden punkt wspólny z wykresem tej konkretnej funkcji. Nie można milcząco zakładać oczywistości tego, co oczywiste nie jest.

===: ... piłeś coś dzisiaj ...

Olga: π......

PW: Wolę argumenty naukowe. Zastanów się jeszcze raz nad tym co napisałem. Twoje rozwiązanie zawiera błąd logiczny i nie może być stawiane za wzór.

===: ... wystarczy, że za wzór postawimy ciebie ...

PW:

	1
No to teraz przeczytaj uważnie zadanie jeszcze raz. Narysuj wykres y =		, x> 0 oraz
	x

wykres prostej y = x −5. Wykres funkcji i prosta mają jeden punkt wspólny. Prosta i osie układu wyznaczają trójkąt. Ten trójkąt też ma pole 2? Teza postawiona w zadaniu jest fałszywa. Nie ma powodów, żeby rozwiązujący poprawiał treść zadania "w rozumie", ani żeby przyjmował coś "na wiarę".

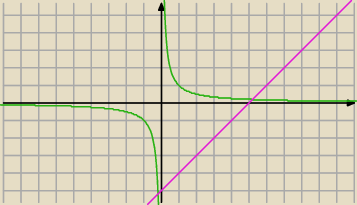
WP: a czy y=x−5 ma jeden punkt wspólny z wykresem funkcji ?

PW: Nie doczytałeś warunków zadania, czyli rozwiązujesz swoje zadanie − inne niż chciał autor. Napiszę w takim razie jeszcze raz: wykres funkcji

	1
y =		(x>0).
	x

Tak stoi w treści zadania. Nie poprawiamy treści i nie domyślamy się, co autor mógł mieć na myśli, a zapisał źle.

===: ... ja rozwiązuję swoje ....ty swoje ... i jak zwykle wszystko ma być tak jak ty to ogarniasz. Pozostań gwiazdorku przy swoim i czuj się z tym dobrze ... tylko nie pouczaj ... Nikt tu twoich nauk nie oczekuje. Nie dociera do ciebie i nie dotrze, że to zadanie wedle twego "rozumowania" sensu nie ma.

PW: Masz przykrą tendencję do obrażania przeciwnika, gdy brakuje argumentów. W żadnym miejscu nie obrażałem Cię ani nie sugerowałem alkoholizmu czy „gwiazdorstwa”. Nie interesuje mnie to, czy myślisz poprawnie, czy nie. Jak dla mnie to możesz umrzeć w przekonaniu, że prosta mająca jeden punkt wspólny z wykresem to styczna i na odwrót. Rozwiązuj dalej "swoje"., ale nie gryź myślących inaczej. Każdemu zdarza się coś źle zrozumieć, ale o klasie człowieka świadczy to, czy potrafi się do tego przyznać. Ponieważ nie cierpię chamstwa, obiecuję tu więcej nie zaglądać i omijać wszelkie posty, w których występuje "===". Już dalej się nie wysilaj, ja na pewno tego nie przeczytam.

===: ... no cóż ...chama to masz przed monitorem

Eta: Ejj Panowie przez duże P wyluzujcie! Przedstawiam takie rozwiązanie tego zadania: ( nic nie wspominając o stycznej

	1
dowolna prosta y= ax+b i krzywa y=		dla x>0
	x

mają mieć jeden punkt wspólny, to

	1
ax+b=		⇒ ax2+bx−1=0 warunek Δ=0
	x

	1
Δ= b2+4a =0 ⇒ a= −		b2
	4

zatem prosta ma równanie :

	1		4
y= −		b2+b , AOX=(		,0) i BOY(0,b)
	4		b

pole trójkąta ograniczonego tą prostą i osiami układu :

	1		4
P=		*		*b= 2 [j2]
	2		b

Pozdrawiam

Eta: Poprawię jeszcze chochlika: zatem prosta ma równanie: y= −¹₄b²x+b

Eta: