przebieg zmienności funkcji kyrtap: Mila pomożesz ?

52: Pisz śmiało ja pomogę jak będę umiał

kyrtap: mam funkcję f(x) = (x−1)²(x+2)

52: i co konkretnie ?

kyrtap: badam Df = R Funkcja f jest ciągła na R bo jest wielomianem. miejsca zerowe wiadomo wiadomo też że trzeba policzyć f(0) aby sprawdzić w jakim punkcie przetnie oś y i teraz pytanie co z parzystością i okresowością

kyrtap: muszę zawsze to badać?

52: Mnie kiedyś uczono aby badać....

kyrtap: czyli co badam f(−x) tak?

52: f(−x)=f(x) parzystosc f(−x)=−f(x) nieparzystosc

kyrtap: no wiem tylko pytam

kyrtap: czy badać to

kyrtap: ok będę badać

Mila: Jutro, padam. Dobranoc, trzeba było wcześniej .

52: badać zawsze się przyda

kyrtap: potem obliczam granice w −∞ i ∞ si?

kyrtap: Mila spokojnej nocy, wypoczywaj

52: Si

kyrtap: dobra liczę sobie narazie jak coś będę pytał

kyrtap: dobra teraz muszę znaleźć asymptoty, tak na dobrą sprawę ja wiem że jeśli dziedzina jest na R to nie ma asymptot pionowych a co z poziomymi i ukośnymi muszę liczyć tak

	f(x)
a = lim x →∞
	x

	f(x)
a = lim x →−∞
	x

b= lim _{x →∞} (f(x) − ax) b= lim _{x →−}∞(f(x) − ax)

52: tak

kyrtap: te wpółczynniki a i b muszę też liczyć w −∞

52: pasowało by Tylko że przeważnie to wyjdzie to samo co w ∞, także myśl przy tym

kyrtap: no właśnie niektórzy piszą tylko w ∞ a niektórzy i w tym i w tym więc nie wiem

razor:

	f(x)
a1 = limx→∞
	x

b₁ = lim_x→∞ f(x) − a₁x

	f(x)
a2 = limx→−∞
	x

b₂ = lim_x→−∞ f(x) − a₂x jeśli a₁ i b₁ lub a₂ i b₂ będą liczbami to proste a₁x+b₁ lub a₂x+b₂ będą asymptotami

kyrtap: widzę razor nocyn Marek

kyrtap: nocny*

razor: wstałem o 2

john2: Pan w e−trapezie mówił, że punkty przecięcia z osiami, parzystość, nieparzystość, okresowość są tylko pomocnicze, choć należy te rzeczy też zbadać. Jednak jeśli np. licząc miejsca zerowe, wylądujesz z nierozwiązywalnym konwencjonalnymi metodami równaniem wielomianowym, po prostu pomijasz ten krok.

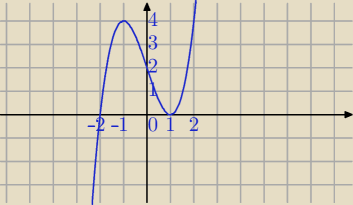
Mila: f(x)=(x−1)²*(x+2) 1) D=R 2) miejsca zerowe f(x): (x−1)²*(x+2)=0⇔ x−1=0 lub x+2=0 x=1 lub x=−2 3) granice na krańcach dziedziny lim_x→−∞(x−1)²*(x+2)=−∞ lim_x→∞(x−1)²*(x+2)=∞ Asymptot poziomych brak. 4) asymptoty ukośne :

	(x−1)2*(x+2)
limx→∞		=∞
	x

	(x−1)2*(x+2)
limx→−∞		=∞
	x

asymptot ukośnych brak 5) Pochodna f'(x)=2*(x−1)*(x+2)+(x−1)²*1 f'(x)=(x−1)*(2x+4+x−1)=3*(x−1)*(x+1) 6) miejsca zerowe pochodnej f'(x)=0⇔ x−1=0 lub x+1=0 x=1 lub x=−1 kandydaci na ekstrema 7) zmiana znaku pochodnej f'(x)>0⇔x<−1 lub x>1 8) monotoniczność f(x) ↑dla x<−1 , f(x)↓dla x∊<−1,1>, f(x)↑dla x>1 x=−1 maksimum lokalne f(−1)=4, x=1 minimum lokalne f(1)=0 ========================= Wykres

kyrtap: ja tak na dobrą sprawę obliczam Mila jeszcze drugą pochodna aby znaleźć punkt przegięcia no i sprawdzam parzystość funkcji

kyrtap: mam nadzieję że to co robię nie jest błędem

Mila: Tak, trzeba to zrobić. Jeszcze trzeba napisać, gdzie funkcja wypukła, a gdzie wklęsła.

kyrtap: wszystko piszę

kyrtap: a mam pytanie Mila? bo w szkole liceum pisało się że funkcja jest rosnąca lub malejąca na przedziale domkniętym a tutaj w książkach jest przedział otwarty gdy się liczy f'(x) >0 i f'(x) < 0 możesz to mi wyjaśnić?

Mila: To kwestia umowy, zobacz jak podali na wykładzie, albo w aktualnym podręczniku. Ostatnio pytają w zbiorach o maksymalny przedział w którym funkcja jest np. rosnąca.

kyrtap: W podręczniku monotoniczność funkcji jest podawana w przedziałach otwartych

Mila: To pisz otwarte, mnie też uczono, że pisze się otwarte.

kyrtap: ok

Gray: Cześć Mila, cześć kyrtap Jeżeli pytają o maksymalny przedział w którym funkcja jest np. rosnąca, to jeżeli jest rosnąca na [a,b] to należy napisać [a,b], a nie (a,b). W sensie długości przedziału, czy liczby elementów przedziały [a,b] i (a,b) są identyczne, ale w sensie inkluzji już nie, więc w tym sensie większy jest [a,b]. A rzecz jest bardzo prosta: przy pomocy pochodnej stwierdzamy, że f jest np. rosnąca na (a,b). Jeżeli wiemy, że f jest ciągła w a oraz w b, to f jest wówczas rosnąca na [a,b]. Jeżeli ciągłości nie ma, monotoniczność może się popsuć (ale nie musi). Wtedy należy granicę w punktach a oraz b porównać z wartością f(a) oraz f(b). Jeżeli f(a) jest mniejsza lub równa niż lim_x→a⁺f(x) to jest rosnąca na [a,b); jeżeli nie, to nie. Podobnie robimy z punktem b. W większości przypadków funkcja jest jednak ciągła, wtedy nie ma tej dyskusji.

kyrtap: Gray mam pytanie podrzuciłbyś jakiś przykład w której funkcja jest nieciągła to bym przeanalizował to z tymi domknięciami

Gray: Podrzucę, ale to chwilę potrwa, bo księdza ma za chwilę... Chyba to dziś...

kyrtap: ok powodzenia

Gray: Dzięki. Na szybko, ale pamiętam, że miłe zadanie: zbadaj monotoniczność funkcji f(x) = [x+1]^x + x^x + x^[x] + [x]^x. Powiedzmy na przedziale (0,4), chociaż jak chcesz możesz powalczyć na x>0. Oczywiście [x] to cecha z x.

Gray: Bardziej normalne podam później (jeżeli będziesz jeszcze chciał).

kyrtap: będę

Mila:

Gray: Wyznacz największe przedziały monotoniczności funkcji f określonej wzorem:

	⎧	x2+2x, gdy x>1
	⎜	1, gdy x=1
f(x)=	⎨	x/(x2+1), gdy x∊(−1,1)
	⎩	−x2−2x+1, gdy x≤−1

Służę pomocą. To z 18:13 nie jest trudne (rozbij na przedziały), ale wymaga ostrożności w punktach x∊N.

kyrtap: Dzięki wybacz ale jutro zabiorę się za to bo muszę jeszcze projekt zrobić dzisiaj

Gray: Ja znam rozwiązanie; zadanie jest dla Ciebie, więc pośpiechu nie ma. Jedna rada − spróbuj rozwiązać bez rysowania wykresu − same rachunki i wnioski.

kyrtap: mogę tabelkę pomocniczą zrobić?

Gray: Pozwalam. Ależ mam moc...

kyrtap: moc nauczania