Problem z geometrią

Problem z geometrią Arcyksiąże: Znaleźć równanie okręgu opisanego na trójkącie ABC o wierzchołkach A = (0, 0), B = (8, 0), C = (0, 6). Jakiś sposób na to zadanie ?

9 sty 00:07

kyrtap: taka podpowiedź środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych trójkąta

9 sty 00:11

Mila:

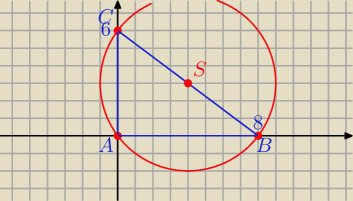
I Równanko: (x−a)²+(y−b)²=r² S=(a,b) to będzie środek BC S=((4,3)

	1
r=		BC
	2

r=5 Pisz.

9 sty 00:15

Arcyksiążę: Równanie z 3 niewiadomymi ?

9 sty 00:24

Eta: Ejj ... Wasza Wysokość emotka

ten trójkąt jest prostokątny!

9 sty 00:27

Arcyksiążę: Moja królowo proszę mnie tak nie tytułować ! A skąd mam to wiedzieć tak od razu ?

9 sty 00:28

Mila: Układ współrzędnych jest prostokątny. A Δ pitagorejski , boki 6,8,10 (x−4)²+(y−3)²=5²

9 sty 00:35

Arcyksiążę: Dziękuję, teraz dokończę.

9 sty 00:45