Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym
ninaxx: Podpowie ktoś jak sie wgl. za to zabrać?
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym o mierze
łukowej α. Kąt ten jest oparty na cieciwie o długości a. Oblicz objętość tego stożka
8 sty 21:08
Eve:
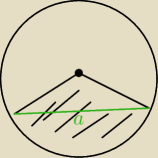
8 sty 21:14
ninaxx: I co z tym dalej?
8 sty 21:29
Eve: masz wynik?, bo coś obliczyłam, ale strasznie długie wyrażenie wyszło?
8 sty 21:44
ninaxx: wyniku nie mam, ale z tego co pamietam to nie był on tak bardzo skomplikowany bo profesor mi go
pokazywał
8 sty 22:02
Eve: mnie wyszło cos takiego
| 1 | | α2 | | a3(tg21/2α+1) | |
| π |
| * |
| |
| 3 | | 900 | | 8tg21/2α | |
8 sty 22:10
ninaxx: ciężko mi stwierdzić czy tak to było, a mogę wiedzieć jak to rozwiązałaś?
8 sty 22:14
Eve: | 2πr | | α | | 720r | |
| = |
| ⇒l= |
| |
| 2πl | | 360) | | 2α | |
wstawiłam l
obliczyłam r i podstawiłam do V
| | 1/2a | | a | |
dodatkowo tg 1/2α= |
| ⇒H= |
| |
| | H | | 2tg1/2α | |
i to tez do wzoru na V
doprowadziłam do najprostszej postaci
8 sty 22:27
pigor: ..., widzę to tak : niech z warunków zadania
Vs=13π r2H=?,
α − miara kąta środkowego
w radianachdanego wycinka kołowego
o promieniu l (el), którego długość to zarazem tworząca stożka taka,
że
a=α*l =2πr − długość łuku danego wycinka i obwód podstawy
| | a | | a | |
stożka ⇒ l= |
| oraz r= |
| , więc kwadrat |
| | α | | 2π | |
| | a2 | | a2 | |
wysokości stożka H2=l2− r2= |
| − |
| = |
| | α2 | | 4π2 | |
| | a2(4π2−α2) | | a | |
= |
| ⇒ H= |
| √4π2−α2, |
| | 4α2π2 | | 2απ | |
| | 1 | | a2 | | a | |
stąd i z (*) : Vs= |
| π * |
| * |
| √4π2−α2 = |
| | 3 | | 4π2 | | 2απ | |
| | a3 | |
= |
| *√4π2−α2, czyli |
| | 24απ2 | |
| | a3√4π2−α2 | |
Vs= |
| − szukana objętość stożka.  |
| | 24απ2 | |
8 sty 22:56
ninaxx: w sumie zastanawia mnie czym właściwie jest to "a", rozumiem że jest ono dł. cięciwy ale ta
cięciwa czemu odpowiada w stożku?
8 sty 22:57
pigor: ... , o kurde, u mnie
a to długość łuku, a nie cięciwy ;
czyli rozwiązałem ...

inne zadanie; przepraszam . ...

8 sty 23:00
pigor: .., no właśnie dobre pytanie i być może miała to być
długość łuku na którym opiera się dany kąt środkowy . ...

8 sty 23:03
Eve: no nie koniecznie,kąt może opierać się na cięciwie
8 sty 23:06
pigor: ..., nie no jasne, że może, ale autor postu podaje "z pamięci" treść zadania
i pisze o godzinie 22 : 02 tak: ,
"wyniku nie mam, ale z tego co pamiętam to nie był on tak bardzo skomplikowany
bo profesor mi go pokazywał" , a więc u niego to cięciwa, a może to był ...

łuk
9 sty 00:57


 inne zadanie; przepraszam . ...
inne zadanie; przepraszam . ...

 łuk
łuk