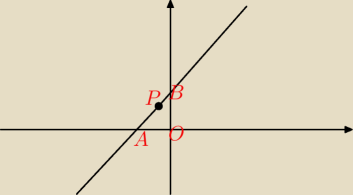
Prosta, geometria analityczna, analiza matematyczna hajnów: Prosta k: y=ax + b gdzie a>0, orzechodząca przez punkt P(−1,2) odcina na osiach układu współrzędnuch odcinki których suma długości jest najmniejsza. Wyznacz równanie tej prostej Odcinek |OB| to wartość y dla x=0 czyli y=b Odcinek |OA| to wartość x dla y=0 czyli x=^−b_a Prosta przechodzi przez punkt (−1,2) czyli 2=−a+b ⇒ a=b−2 czyli w |OA| to x=^−b_b−2 Suma − S= b − ^b_b−2 = ^b2−2b−b_b−2=^b2−3b_b−2 b≠2 Pochodna = ^{(2b−3)(b−2)−(b2−3b)}_(b−2)² = ^b2−4b+6_(b−2)² I tutaj dalej nie wiem bo Δ<0 co robię źle ?