Zadnia optymalizacyjne, ekstrema Dostateczny: Prosta K:y=ax+b gdzie a>0, przechodząca przez punk P=(−1,2) odcina na osiach układu współrzędnych odcinki, których suma długości jest najmniejsza. Wyznacz równanie tej prostej. Mógłby ktoś podpowiedzieć jakie oznaczenia, bo cały czas mam dwie niewiadome

Dostateczny: ma ktoś jakiś pomysł?

dwiq: y=ax+b 2=−a+b a=b−2 Jeden odcinek x=0 czyli y=b Drugi odcinek y=0 czyli 0=ax+b czyli x=−b/a a a=b−2 czyli x=−b/b−2 Suma to b − b/b−2

Dostateczny: ok, ale potem mam problemy z wyliczeniem miejsc zerowych

dwiq: to nie wiem, wydaje mi się, że powinno być dobrze, a co delta nie wychodzi równa czy pochodną nie umiesz wyliczyć ?

dwiq: *nieładna

Dostateczny: pochodna wyliczyłem, ale potem Δ<0 pochodna podaje możesz sprawdzić: =(b²−4b+6)/(b−2)²

dwiq: no tak w rzeczywistości Δ<0; to nie wiem, muszą się mądrzejsi wypowiedzieć

===: y=ax+b 2=−a+b ⇒ b=a+2

	ax		y
y=ax+a+2 ax+y=−a−2		+		=1
	−a−2		−a−2

	x		y
		+		=1
	−a−2   a		−a−2

	−a−2		2
Suma S=		−a−2=−3−a−
	a		a

	2		−a2+2
S'=−1+		=
	a2		a2

S'=0 ⇒ a²=2 itd...

===:

Dostateczny: dziękuję, a po co te przekształcenia (ax)/ −a−2 +...?

===: ... a równanie prostej w postaci odcinkowej pamiętasz?/znasz?

Dostateczny: oj nie, w ogóle pierwszy raz słyszę

===: to wpisz w przeglądarkę −

===:

x		y
	+		=1
a		b

zeneg: A skąd tą sumę wziąłeś, dlaczego ona się równa a+b= ?

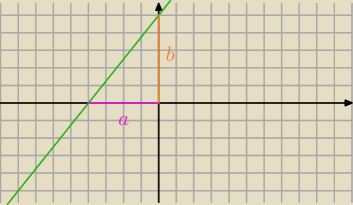
===: bo a to odcinek odkładany na osi 0x zaś b na osi 0y

x		y		x		y
	+		=1 na wykresie masz		+		=1
a		b		4		5