Rozwiąż nierówność Kasia: x³−9x≤0 x(x²−9)≤0 :x x²−9≤0 √ −√9≤0 −3≤0 Dobrze jest? Bo ja nie umiem matmy a zależy mi żeby było dobrze.

J: jest tragicznie, na jakiej podstawie podzieliłaś przez x ..? dalej jeszcze gorzej ...

Dawid: Rozwiązaniem nierówności jest jakiś przedział x(x²−9)≤0 i niżej już jest źle

Dawid: x(x²−9) x(x−3)(x+3)

Kasia: Dzięki wielkie. Ja z tej matematyki nic już nie pamiętam. I nigdy też nie umiałam dobrze matmy. A nie chciałam nic nie policzyć i prosić o gotowca

Dawid: Ale to jeszcze nie koniec teraz Twoja kolej na dokończenie

Kasia: Spróbuję Za chwilkę wyślę

Dawid: Czekamy z niecierpliwością 

Kasia: x(x−3)(x+3) (x²−3x)(x+3) x³−3x²−3x²−9 x³−6x²−9 Zacięłam się to pewnie źle zrobiłam.

J: .. a słyszałaś coś o rysowaniu "wężyka" ...?

Kasia: nie

Kasia: a o to chodzi }?

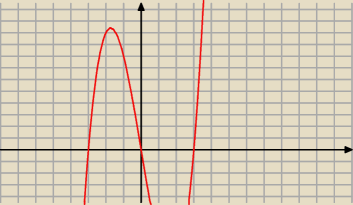
Dawid: Tragedia, nawet źle wymnożone. Nawet gdybyś dobrze wymnożyła to byś wróciła do postaci x³−9x, a oto tutaj nie chodzi mamy znaleźć taki x które będą spełniać tą nierówność x³−9x≤0 dlatego obliczenia wyglądają tak: x³−9x≤0 x(x²−9)≤0 x(x−3)(x+3)≤0 Mamy postać iloczynową więc łatwo możemy odczytać miejsca zerowe wystarczy, że przyrównasz do zera x=0 i x−3=0 i x+3=0 x=0 i x=3 i x=−3 I to są nasze rozwiązania teraz rysujemy wykres. Rysujemy go od prawej strony od góry bo współczynnik przy najwyższej potędze jest dodatni więc wykres wygląda tak jak u góry. Teraz odczytaj rozwiązanie

Kasia: Jejku nie pamiętam a nie chce znów gafy strzelić jak przedtem Rozwiązaniem równania jest przedział liczb tak?

Dawid: tak

Kasia: Ale nie z dwoma nawiasami nie? Spróbuję tylko proszę mi głowy nie urywać bo ja naprawdę nie pamiętam matmy <−3,3)−−>tak?

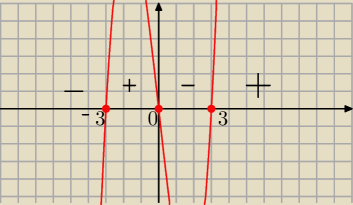
Dawid: Teraz odczytasz ?

Kasia: (−∞+3) (∞−3) o to chodziło?

Dawid: Pierwszy przedział jest prawie dobrze tylko nawias ma być domknięty bo mamy znak ≤ Zatem (−∞,−3>U<0,3>

Kasia: Dzięki wielkie Podziwiam takich geniuszy matematycznych jak ty

5-latek: Takim samym geniuszsem mozesz byc Ty . Tylko odrobine wiecej pracy wlozyc