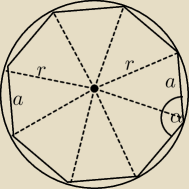
Ośmiokąt Metis: Wykaż, że jeśli bok ośmiokąta foremnego ma długość a, to promień okręgu opisanego na tym

	a
ośmiokącie jest równy		√4+√8
	2

	(n−2)*180o		(8−2)*180o
α=		=		= 135o
	n		8

Nie widzę z jakich własności mogę to dowieść Jak to widzicie ?

Metis: Jednak mam Na podstawie twierdzenia cosinusów: a²=r²+r² −2r² * cosβ cosβ= 360^o :8 = 45^o Stąd: a²=r²+r² −2r² *cos45^o I po uproszczeniu wychodzi

Saizou :

	360
x=		=45o
	8

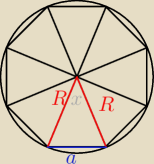
z tw. cosinusów a²=R²+R²−2R²cos45

	√2
a2=R2(2−2*		)
	2

a²=R²(2−√2)

	2−√2
R2=
	a2

	√2−√2
R=
	a

Metis: Dzięki Saizou trochę sie rozpędziłem, nie wiedziałem, że zadanie "samo się rozwiąże" Masz trochę czasu ?, mam jeszcze jedno zadanko z planimetrii.

Mila: Dysgrafia?

Mila: Pisz Metisku, abyś dostał piątkę.

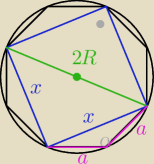
Saizou : można też tak

	x√2
x z tw. cosinusów 2R=x√2⇒R=
	2

Metis: Nie stawiają za pracę domową Ale sprawdzian w poniedziałek więc powoli powtarzam

Mila: Saizou, sprawdź R w poprzednim zadaniu 21:11.

Saizou : odwrotnie zapisałem, no ale to rachunek, zresztą Metis jest bystry i się by skapnął

Metis:

Saizou : Metis zadanko extra, wykaż wzór na wyróżnik trójmianu kwadratu i pierwiastki wielomianu 2 stopnia

Metis:

Saizou : czekam do 21:50

Saizou : no i jak ?

Metis: http://wstaw.org/m/2015/01/07/Zadanie10.png Wykaż, że miara kąta EDF = α, gdzie α to kąt ostry równoległoboku.

Metis: Przyznaj że piękny rysunek

Saizou : ∡ADC=180−α=90−α+β+90−α⇒β=α

Saizou : tak, ale przy F nie masz 90^o

Metis: Kurczę, już to poprawione Dzięki Saizou

Saizou : ja nadal czekam na deltę

Metis: Delty Ci nie wyprowadzę Ale ze wzorów na pierwiastki można ją wskazać

Saizou : a ja chcę wyprowadzenie rozważ wielomian ax²+bx+c=0 i kombinuj ze wzorkiem (d+k)²=d²+2dk+k²

Metis: A rysunek jednak dobrze |DF| to wysokość , a kąt miedzy |DF| a |PF| ma być

Saizou : ale na Twoim rysunku kąt β nie ma 90^o, bo geogebra ma ustawiona że z automatu eksponuje kąty proste można to zmienić, ale kto by się w to bawił

Metis: Saizou poźno jest A jutro muszę wstać na 5 Poza tym jeszcze kodeks drogowy do opanowania

Metis: Racja. Ustawiłem to "ręcznie"

Saizou : Metis piona ja też wstaję o 5 prawko ?

bezendu: Kodeks drogowy taki prosty

Metis: Ty o 5 ? Nie za wcześnie na studenta? Tak, jeżdżę już po mieście, a rozpocząłem przed 18 − 3 miesiące przed

Saizou : no to powodzenia, trzymam kciuki, teoria jest prostsza, (jak dla mnie), w sumie jazda też jest łatwa, ale nie można się stresować, eh.... nie lubię egzaminów ale nie zasłaniaj się kodeksem, tylko wykaż deltę

bezendu: wypij browara przed egzaminem

Saizou : a no tak, muszę dojechać na uczelnie, na to zad...e gdzie już psy nawet nie szczekają tylko dziki swawolnie latają po kampusie

Metis: bezendu cenne rady Saizou to wiem co czujesz Ogółem to teraz trochę się pozmieniało w prawie jazdy. Doszła ekonomiczna jazda. Podskoczyła cena egzaminów.

Saizou : to ile teraz kosztuje egzamin ?

Metis: Zapłaciłem 1400 z czymś + badania. Przed nowym rokiem było około 1240 zł.

Saizou : 1400 za kurs+ badania, ale cena egzaminu to nadal 170 zł (P+T)

Metis: A fakt, przepraszam nie sprecyzowałem. Chodziło mi oczywiście o kurs prawa jazdy. Cena egzaminu w WORDzie chyba bez zmian

Saizou: cena kursu jest ustalana przez osrodek w ktorym sie uczysz, a egzamin jest panstwowy i ceny sa wszedzie takie same xd a teraz lece spac, i jutro cie pomecze z delta

Metis: Na razie

Saizou : hihih... czekać na deltę

Saizou : Cięgle czekając.....

Metis:

Saizou : no zaczynamy dowód: rozważmy równanie w postaci ax²+bx+c=0 gdzie a≠0.....

Metis: Jeśli równanie przyjmuje postać ax²+bx+c=0 , a≠0 i x∊R to równanie jest równaniem kwadratowym

Saizou : tak, ale co mamy do pokazania ?

Saizou : posiłkuj się wzorem (k+l)²=k²+2kl+l²

Metis: Pokazać mamy deltę tak ?

Saizou : tak... no i działasz, to nic trudnego, zabawa na wzorkach skróconego mnożenia

Metis: k²+2kl+l²=0 /4 4k²+8kl+4l²=0

Metis: ax²+bx+c=0 4ax²+ 4bx+4c=0 4ax²+4bx=−4c 4a²x+4abx=−4ac

Saizou : ja proponuję tak ax²+bx+c=0

	b		c
x2+		x+		=0 i teraz ze wzorku s.m
	a		a

Metis: 4a²x+4abx=−4ac /+b² 4a²x+4abx + b²= −4ac+b² 4a²x+4abx + b²= b²−4ac 4a(x+bx)+b² = b²−4ac

Metis: Jest i delta, ale co z lewą stroną ?

Saizou : no właśnie, co z lewą stroną jakiego znaku powinno być to wyrażenie ?

Metis: Tutaj widzę teraz błąd źle wyłączyłem przed nawias: 4a(ax+bx)+b² Oczywiście wyrażenie nieujemne.

Saizou : a skąd to twierdzisz ?

Metis: Nie no nie ma tutaj wzorku

Saizou : no właśnie, a teraz mykam, pokombinuj raz jeszcze

Metis: Pokombinowałem i ... znalazłem błąd rachunkowy //Poprawiam 4a2x²+4abx=−4ac / +b² 4a2x²+4abx+b² = −4ac+b² (2ax+b)²=b²−4ac (2ax+b)²=Δ Samo kombinowanie z tym wyprowadzaniem Najprościej byłoby wskazać ją we wzorze na pierwiastki dwumianu, w końcu Δ to tylko oznaczenie wyrażenia o postaci b²−4ac

Saizou : ale te pierwiastki wzięły się z tego że istnieje delta (2ax+b)²=Δ /√ l2ax+bl=√Δ 2ax+b=±√Δ 2ax=−b±√Δ

	−b±√Δ
x=
	2a