parametr Kinga : Zbiorem rozwiązań nierówności ^2x+m−2_X−3 ≥ mx jest zbiór (−∞, 0> <3,4>. Wtedy wartość parametru m jest równa?

Eve: jakim cudem 3 należy do zbioru rozwiązań? pamiętaj cholero nie dziel przez zero

Kinga : Właśnie też mnie to Zdziwiło i Jeszcze to ze oni oczekują konkretnej wartości m a moim zdaniem powinien być to przedział

5-latek: No to przedzial <3,4> daj taki (3,4>

Eve: ale jeśli w zadaniu jest podaj wartość, to nie musi oznaczać konkretnej

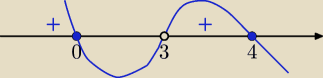
Bogdan: Istnieje konkretna wartość m spełniająca warunki zadania: x∊(−∞, 0>∪(3, 4>. m = 2.

Kinga : Tak musi bo to zadanie zamknięte i są 4 wartości do wyboru a.1 b.4 c.2 d.−3

Kinga : Jak to wyliczyć?

Eve: w tym wypadku tak, ale czasem takie pytanie pada, podaj wartości i może byc przedział

Kinga : Jak mi ma wyjść wartość jak cały czas wychodzi mi przedział?

Bogdan:

2x + m − 2		2x + m − 2 − mx2 + 3mx
	− mx ≥ 0 ⇒		≥ 0
x − 3		x − 3

Przechodzimy do nierówności równoważnej: −(mx² − (3m + 2)x − m + 2)(x − 3) ≥ 0 Są trzy pierwiastki: 0, 3, 4. Pierwiastek 3 zawiera czynnik (x − 3), pozostałe pierwiastki: 0 i 4 zawiera trójmian mx² − (3m + 2)x − m + 2 Tworzymy postać iloczynową: ax(x − 4) = ax² − 4ax, porównujemy współczynniki: m = a, 3m + 2 = 4a, −m + 2 = 0 ⇒ m = 2

Kinga : Wielkie dzięki