Udowodnij równość odcinków (twierdzenie Pitagorasa, przystawanie). MMoon: Na przyprostokątnych BC i CA trójkąta prostokątnego ABC zbudowano na zewnątrz kwadraty ECBD i FGAC. Prosta AD przecina bok BC w punkcie P, a prosta BG przecina bok CA w punkcie R. Wykaż, że odcinki CP i CR mają równą długość.

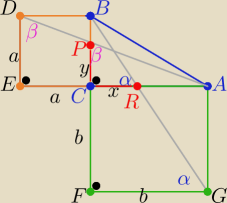
Eta: |CR|=x , |CP|=y , |AC|=|FC|=b , |BC|=|DE|=a Z podobieństwa trójkątów ( z cechy (kkk) GFB i RCB oraz DEA i PCA :

b		b+a		a		a+b
	=		i		=
x		a		y		b

	ab		ab
x=		i y=		⇒ x=y
	a+b		a+b

zatem |CP|= |CR| c.n.u

5-latek: Dobry wieczor Eta TY chyba masz juz gdzies skopiwane te zadania (wiesz jakie beda )

Eta: Witaj "małolatku" Rozwiązuję od ręki ( jak leci) pewnie już może 100−y raz Naszym forumowiczom nie chce się szukać w archiwum( wygodni są

5-latek: Moze za 10 lat tez bede tak rozwiazywal od ręki tak jak Ty

Eta: A zainteresowany milczy jak grób

5-latek: Z tego co mi sie przypomina Moon to ksieżyc . Moze wyje do ksieżyca