TEST II Blue: Bardzo proszę o sprawdzenie mi tych zadań

	n		1
zad.11 Udowodnij nierówność |		−		|< 0,01
	2n−1		2

http://i59.tinypic.com/5mfuvb.jpg

	2−sin22α
zad. 12 Udowodnij tożsamość sin4α + cos4α =		.
	2

http://i58.tinypic.com/9bhtv5.jpg zad.17 Długości boków równoległoboku wynoszą a i b, a długości jego przekątnych m i n. Udowodnij, że a⁴+b⁴ = m²*n² wtedy i tylko wtedy, gdy kąt ostry równoległoboku ma miarę 45⁰. http://i58.tinypic.com/23mlc11.jpg oraz tego: czy ten wykres jest dobrze narysowany? http://i57.tinypic.com/2nbamw3.jpg

Blue: Mila jesteś na forum ? Albo Eta ?

Kacper: Zadanie 11 ok. Zadanie 12 znowu robisz źle! (brak komentarza) − coś nie bardzo rozumiesz przeprowadzanie dowodów.

Kacper: Do wykresu dorysuj asymptotę.

Kacper: Zadanie 17 ok, ale znowu brak słów i muszę się domyślać czemu w danym momencie liczysz to, a nie tamto.

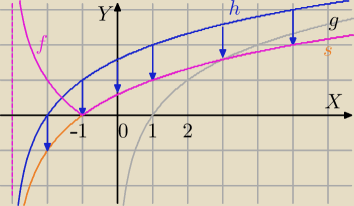
Mila: 16) g(x)=log₂(x)→T_[−3,0]⇔h(x)=log₂(x+3)→T_[0,−1]⇔s(x)=log₂(x+3)−1⇒ Symetria OX dla y<0⇒ f(x)=|log₂(x+3)−1|

Blue: Dlaczego 12 jest źle

Eta: 12/ Masz dojść od lewej strony do prawej lub odwrotnie

	1		2−sin2(2x)
L= (sin2x+cos2x)2−2sin2x*cos2x= 1−		sin2(2x)=		= P
	2		2

Mila: 12) L=sin⁴x+cos⁴x=(sin²x+cos²x)²−2*sin²x*cos²x=

	1		1		2−sin2(2x)
=1−2*(sinx*cosx)2=1−2*[		sin(2x)]2=1−2*		sin2(2x)=		=P
	2		4		2

cnw

Blue: Aha, czyli to nie może być tak robione.... Ale szczerze mówiąc, to i tak widać, że to to samo przez to, co ja zrobiłam...

kyrtap: Takie dowody musisz robić tak jak piszą wyżej eksperci

kyrtap: i pamiętaj o założeniach tutaj

kyrtap: przynajmniej ja jak nie napisałem założeń jeśli chodzi o wykazywanie tożsamości miałem ucinane punkty